4

The function $\operatorname{sinc}{\pi x}$ has maxima and minima given by the function's intersections with $\cos \pi x$, or alternatively by $\frac {d}{dx}\operatorname{sinc}{\pi x}=0$.

Mathematica tells me that

$$\frac {d}{dx}\operatorname{sinc}{\pi x}=\pi \Bigl(\frac {\cos \pi x}{\pi x}-\frac {\sin \pi x}{\pi^2 x^2}\Bigr)$$

So question 1, how do I prove this?

And question 2, how do I derive an equation for all maxima and minima?

Richard Burke
  • 925

2 Answers2

5

Here is a tested scheme for getting the maxima and minima of the sinc function. First of all, we all agree that we should set the derivative of the sinc function to zero. (Note that here I am taking $\text{sinc}(x)=\sin(x)/x$. You can always replace $x$ by $\pi x$). Now, the derivative of $\text{sinc}(x)$ is

$$\frac{d}{dx}\text{sinc}(x)=\frac{x\cos x-\sin x}{x^2}$$

and setting it to zero will lead to the condition

$$x-\tan x=0$$

This problem comes up in many areas of mathematics. The book, An Atlas of Functions, $2^{nd}$ Edition, by Oldham, Myland, and Spanier, Springer, 2009, shows that the the roots of the above equation, call them $r_n$, can be found efficiently by the equivalent relation

$$r_n=n\pi+\arctan(r_n)$$

where $(n-1/2)\pi<r_n<(n+1/2)\pi$. The beauty of this relation is that if always returns a value for $r_n$ that is less than the starting value. Hence, you can start an iteration at the upper limit of $r_n$ and proceed monotonically to the correct result. However, in my own program I simply used a root finder that I am already familiar with. Once you have the roots, you can get the values of the maxima/minima as $y_n=\text{sinc}(r_n)$.

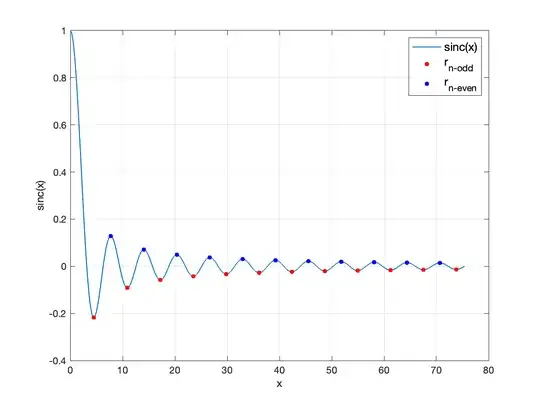
Now, as for which roots are minima and maxima, well, odd-$n$ are minima and even-$n$ are maxima. These are shown as red and blue dots, respectively, in the figure below. Also by symmetry, we also have $y_n=\text{sinc}(-r_n)$ (not shown in the figure).

Sinc with minimax

Cye Waldman
  • 8,196
0

Set derivative equal to 0.

You will after some manipulation like multiplying $(\pi x)^2$ and dividing by $\pi$ get $$\pi x \cos(\pi x) = \sin(\pi x)$$ and equivalently by dividing both sides by $\pi x$ $$\cos(\pi x) = \frac{\sin(\pi x)}{\pi x}$$ Now the right hand side is $\text{sinc}(\pi x)$ and left hand side is the function you want to show it should intersect.

So we are done showing where the extrema are.

Now to show which are max and which are min.

Sinc as a function is a multiplication between $\frac{1}{\pi x}$ and $\sin(\pi x)$

On $\mathbb R^+$ the first of these is monotonically decreasing and positive. Sin is periodic and alternating +1 -1. Both functions are continuous. We can now use an argument with theorem of intermediate value to show it will be alternatingly max and min with as many maxes as mins.

mathreadler
  • 26,534
  • But that just takes us back to the original statement, that the maxima and minima are defined by $\cos (\pi x)=\operatorname{sinc}{(\pi x)}$... I'm after a formula that gives the maxima and minima in terms of $x$ - as in "$min=f(x)$ and $max=g(x)$... – Richard Burke Jul 08 '18 at 20:42
  • Ah, ok I thought you just wanted to derive that every point that is either max or min is an intersection with cos. Well, do you know about continouity and theorem of intermediate value? – mathreadler Jul 08 '18 at 20:45
  • Oops. No. Can you help me with that? – Richard Burke Jul 08 '18 at 20:48
  • Apologies if I don't reply for a while; it's getting late in this part of the world. But I would really appreciate some pointers, or a solution - and I promise to respond to comments / answers tomorrow. G'night. – Richard Burke Jul 08 '18 at 20:53
  • @RichardBurke-Ward I sketched a proof for which are min and which are max. You can probably fill in the blanks if you are taking a first calculus course for engineers or something like that. – mathreadler Jul 08 '18 at 20:57
  • Much appreciated, and I understand your proof. But actually what I was after was a way to calculate what those maxima and minima actually are - what are their (x,y) coordinates? I understand how to get to the general statement $\operatorname{sinc}{\pi x}=\cos (\pi x)$. What I don't understand is how to get from there to a set of specific coordinates. – Richard Burke Jul 09 '18 at 09:28
  • @RichardBurke-Ward you can do that by any numeric scheme for equation solving. I doubt you will find any easily expressible algebraic or analytic solution. You can rewrite it as $\pi x = \tan(\pi x)$ if it is more geometric intuitive to you. Curiously enough if you rewrite it $0 = \tan(\pi x) - \pi x$ the $-\pi x$ exactly cancels first Taylor expansion term. – mathreadler Jul 09 '18 at 09:43
  • Thank you. Frustrating! I was really hoping I could define the actual points. Ah well. I'll mark this as answered if no one else steps in over the next hour. – Richard Burke Jul 09 '18 at 10:11
  • At least you can enumerate them, you know roughly where they will be ( one every $\approx 1$ along the real line and so on ), there are many functions which you both can't express solutions exactly and also have not so many clues where they will be. – mathreadler Jul 09 '18 at 12:28
  • I can live with that! Thanks. – Richard Burke Jul 09 '18 at 13:03