1

Given we have $n \in \mathbb{N}$ different colors and a cube. Under the symmetry constraint, that every side must have the same color, there are $n$ ways to color the cube, just the number of colors in the palette. I also figured out, that if I have the restriction to color all but one side in color A and the remaining side in color B, there are $\frac{n!}{(n-2)!}=n\cdot(n-1)$ ways to color it.

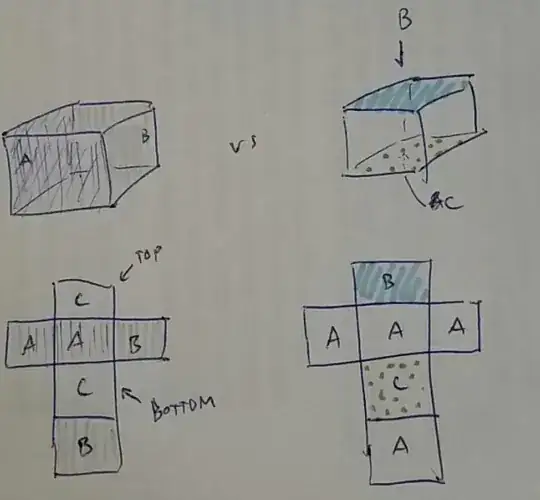
Below I drew two cases that confuse me. The left one has a color C on top and bottom and every two adjacent sides of the hull are of the same color, either A or B. The right has a color B on top and a distinct color C on the bottom with a hull colored in A.

I figured, that I'd start again by $n!$ for all colorings and then divide by the degeneracy. How can I find the number of ways, these objects are the same under rotation? Is there a general way, so I could also solve other symmetry constraints?

enter image description here

It is related to this and this but not the same, since the symmetry constraints are the thing that confuses me. Also found this and this but I'm not sure how and whether that applies to my problem.

ste
  • 331
  • Is it the same as https://math.stackexchange.com/questions/1026/number-of-colorings-of-cubes-faces?rq=1 ? – Dzoooks Jun 27 '18 at 23:40
  • I don't think so. I already mentioned Burnside's Lemma, which is not (nor not straightforwardly) connected to symmetry constraints. – ste Jun 28 '18 at 01:28
  • Could you more clearly state your question? To me, it seemed like you were asking the same question as in the link. – Dzoooks Jun 28 '18 at 02:16
  • My problem has the constraints that the colors A, B, and C are the same. I'm not interested in how many colorings there are with all different or all possible combinations, but only the ones that match e.g. the hull and are distinct in top and bottom coloring (right hand side problem). – ste Jun 28 '18 at 02:37

1 Answers1

1

One way to think of it is to imagine that you have given somebody the cube with the letters pencilled on it, and that they have chosen colours and appropriately painted over the letters. When you get the cube back, can you work out where the letters were?

In the first example, the sides marked C are opposite sides, while the sides marked A adjoin each other, and the sides marked B also adjoin each other. Therefore the colour C can always be determined by inspection. However, A and B cannot be told apart; if we rotate the cube $180^\circ$ around an axis perpendicular to, and through the center of, the C sides, the result is to switch the colours A and B and leave everything else seemingly unchanged. So there are $n$ ways to pick colour C and $\tbinom{n-1}{2}$ ways to pick A and B.

In the second example, we can tell which colour is A because there are four sides that colour. However, turning over the cube swaps sides B and C, leaving everything else seemingly the same, so they are indistinguishable. As a result, there are similarly $n$ ways to pick colour A and $\tbinom{n-1}{2}$ ways to pick B and C.

Normally, that sort of reasoning will be enough. In general, in more difficult cases, what you can do is to systematically turn the cube through every orientation, and see if there is an orientation in which certain letters, or even all letters, have consistently exchanged places (e.g. A↔B or A→B→C→A) while everything else has stayed the same. There are 24 orientations:

  • 1, the original
  • 9 (3x3) rotations around an axis through the centre of a pair of opposite sides
  • 8 (4x2) rotations around an axis through a pair of opposite corners
  • 6 rotations around an axis through the centre of a pair of opposite edges
Andrew Woods
  • 3,707
  • 13
  • 14