21

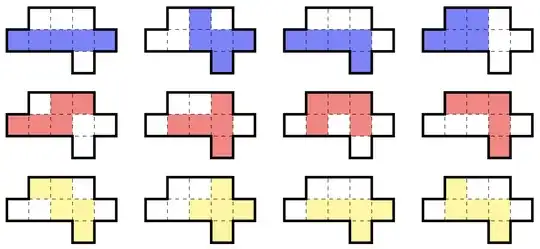
A nine-cell region is the smallest subset of the plane that can contain all twelve free pentominoes, as illustrated below. (A free polyomino is one that can be rotated and flipped.)

A twelve-cell region is the smallest subset of the plane the can contain all $35$ free hexominoes.

Nine-cell region of the plane.

What is the smallest region of the plane that can contain all $108$ free heptominoes (shown below)? All $369$ free octominoes?

free 7-ominos

Also, is there an existing OEIS sequence for this? If not, I'll add one once there is a bit more data. (The sequence begins $1, 2, 4, 6, 9, 12, \cdots$.)

Peter Kagey
  • 5,438
  • If $a(n)$ is the minimum size region covering all $n$-ominoes, then I've constructed examples to show $a(7) \leq 17$, $a(8) \leq 22$ and $a(9) \leq 26$. – Peter Kagey Jun 26 '18 at 20:50
  • And $a(10) \leq 32$. – Peter Kagey Jun 26 '18 at 21:16
  • 1
    You can make the bound $a(n) \leq n \cdot \left\lceil \dfrac{n}{2} \right\rceil$. It's not very good though. –  Jun 26 '18 at 21:19
  • 2
    For the heptomino case, a search over all shapes containable in a $4 \times 7$ bbox only return regions of size $17$. I don't know how to extend the emulation to $5 \times 7$ bbox but this is a strong indication that $a(7) = 17$. – achille hui Jun 26 '18 at 21:40
  • 2
    if I didn' make any mistake, $a(8) \le 20$. example container 00000111-00000111-00111111-11111111 – achille hui Jun 26 '18 at 21:49
  • @achillehui, my program confirmed that this container works, so indeed $a(8) \leq 20$. – Peter Kagey Jun 26 '18 at 22:21
  • I submitted a related computational challenge over at Programming Puzzles & Code Golf Stack Exchange. – Peter Kagey Jun 28 '18 at 19:49
  • 3
    Some upper bounds$$\begin{array}{rcl} n & a(n)\le & \text{example container}\ \hline 7 & 17 & \small\verb/11-111-11111-1111111/\ 8 & 20 & \small\verb/111-111-111111-11111111/\ 9 & 27 & \small\verb/111-111-11111-1111111-111111111/\ 10 & 31 & \small\verb/111-1111-111111-11111111-1111111111/\ 11 & 38 & \small\verb/111-1111-1111-1111111-111111111-11111111111/\ 12 & 43 & \small\verb/1111-1111-11111-11111111-1111111111-111111111111/ \end{array}$$ – achille hui Jun 28 '18 at 20:33

0 Answers0