I want to evaluate following integral:
$\int_{0}^{\infty} \frac {\sin (\ln x) dx }{x^2 + 4} $
Obviously $x$ $ \gt $ $0$ and the function we want to integrate isn't even nor odd. And I need to avoid $0$.
We got two first order poles at $+2i$ and $-2i$
$f(z) = \frac {\sin (\ln z) }{z^2 + 4} = \Im \{\frac {e^{(i\ln z)} }{z^2 + 4} \} $ and we are dealing with a complex logarithm
The residue of the function above for $+2i$ is equal to $res(f, +2i) =\frac {e^{(i Ln 2)}}{4i}$ and I am considering calculating the residue for $-2i$ (it would just switch a sign)
The solution is according to textbook: $\frac {\pi \sin (Ln(2)}{4 \cosh(\pi /2)}$
My questions:
1) How to deal with the integral from $0$ to $\infty$, not from $- \infty$ to $\infty$ in this case. I was used to deal with even functions where it was obvious.
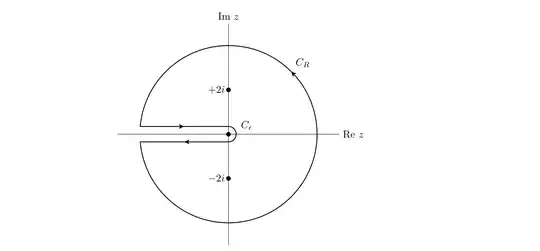
2) I have no clue about the integration path (a semi-circle with branch cuts?)
3) Why that $cosh$ in that solution?
This type of the complex integral is very new to me and I would appreciate any help!