0

I'm learning differential equations recently.Our teacher gave some exercies for us, I did almost all of them but I couldn't understand how to check linear independence , actually I have studied some examples but this questions are looks different for me.

If anybody can show way or any example about them i will be so happy, it's urgent for me.

Check linear independence of the function :

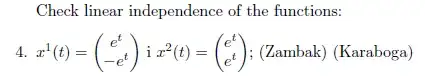
Question 4

Check that the functions are linearly independent solutions of the system. Find the general solution of the system and a fundamental matrix.

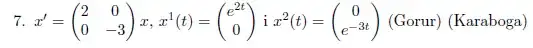
Question 7

thank you :)

Dylan
  • 16,934
Baran KARABOGA
  • 1
  • I'm not sure how your teacher in particular wants you to approach this, but two functions can be shown to be independent (or not) by taking their cross product. If the cross product is non-zero they are independent. If it is zero, they are dependent. – bob.sacamento Jun 12 '18 at 14:16
  • @bob.sacamento What do you mean by "cross-product" of two functions? – user539887 Jun 12 '18 at 14:42
  • @bob.sacamento Thank you but I can't get point sorry ,can you explain what is cross-product. – Baran KARABOGA Jun 12 '18 at 14:55
  • @BaranKARABOGA I put it below as a full answer. Let me know if you have any further questions. – bob.sacamento Jun 12 '18 at 15:10
  • To give a complete answer: I think that in your first problem the best way is just to apply the definition. Let $\alpha, \beta\in\mathbb{R}$ be such that $\alpha x^1(t)+\beta x^2(t)=0$ for all real $t$. From the equality of the first coordinates it follows that $\alpha+\beta=0$, and from the second coordinates you get $-\alpha+\beta=0$. Consequently, $\alpha=\beta=0$, so $x^1(\cdot)$ and $x^2(\cdot)$ are linearly independent. – user539887 Jun 12 '18 at 19:59
  • Regarding the second question: Start by showing that the vector functions are solutions of the ODE system, then prove (in a way as above, for instance) that they are linearly independent. And you are done, because fundamental matrices of two-dimensional systems of linear homogeneous ODEs are just those whose columns are linearly independent solutions of the system. – user539887 Jun 12 '18 at 20:02

1 Answers1

-3

If $\displaystyle x(t) = \left (\array{x_1(t) \\ x_2(t)} \right) \hbox{and } y(t) = \left (\array{y_1(t) \\ y_2(t)} \right )$

then take the cross-product of the two functions, which is: $x_1(t)y_2(t) - x_2(t)y_1(t)$

If this is zero, the functions are dependent. If it is non-zero, the functions are independent.

bob.sacamento
  • 4,112
  • First of all, this is not "cross-product", but Wronskian. Second, the Wronskian of two vector functions being zero is equivalent to their linear independence if they are solutions of some two-dimensional system of linear homogeneous ODEs. In general, that needn't be so, see, e.g., Question about linear dependence and independence by using Wronskian. – user539887 Jun 12 '18 at 15:19
  • The first derivative does not at all come into play in the OP's question, nor in my answer. So, no, this is not at all a Wronskian. The OP was given the task of determining the linear independence of functions that are vectors with two components. That is the question I have addressed. And $x$ and $y$ as I have described here must be independent if their ... anti-symmetric product (or whatever you want to call it, except for "Wronskian", since that's not what it is) is non-zero. And if that product is zero, they cannot be independent. – bob.sacamento Jun 12 '18 at 16:20
  • The name for the determinant of the matrix formed from (column-)vector functions is Wronskian, too. If you take two vector functions, $[\lvert t\rvert,\ t]^{\top}$ and $[t,\ \lvert t\rvert]^{\top}$, their Wronskian is constantly equal to zero. Are they linearly dependent? – user539887 Jun 12 '18 at 19:18