0

With reference to this post,

A conjecture related to Viviani's theorem,

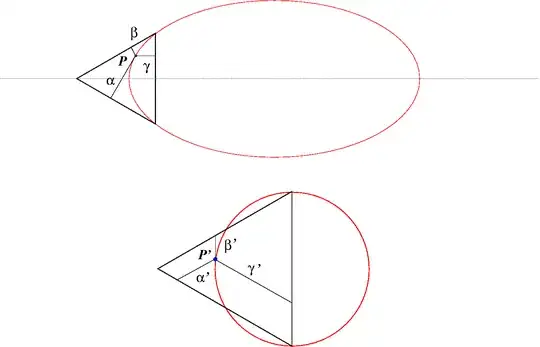
From ellipse to circle in a Viviani's theorem framework

it was suggested (thanks to user Aretino) that, in the top picture (where the triangle is equilateral and the ellipse pass through two vertex of the triangle and tangent there to two sides), $P$ belongs to the arc of ellipse if $\gamma^2=2\alpha\beta$. Here, $\alpha,\beta,\gamma$ are the segments whose lengths are the distances of $P$ from each side.

My first question is:

How can I prove this?

The second question is related to the second picture:

Does $P'$ belong to the arc of circle if and only if $\gamma'^2=2\alpha'\beta'$?

Notice that, in the first picture the segments $\alpha,\beta,\gamma$ sum up to the altitude of the triangle, whereas, in the second one, the segments $\alpha',\beta',\gamma'$ sum up to the side of the triangle.

The most general issue is:

Is there any relationship between the two scenarios?

  • The link and picture are nice. Though, it would be nice if you explained the picture more (e.g. it is assumed that the lines are tangent to the ellipse). Triangle is equilateral and $\alpha,\beta, \gamma$ are actually lengths (even in the original post, it was not so clear). – quantum Jun 05 '18 at 08:15
  • True, I edit these info immediately. Thanks for the remarks! –  Jun 05 '18 at 08:16
  • I gave a proof editing my answer to the original question. A slight change to that proof will also answer your second question. – Intelligenti pauca Jun 05 '18 at 10:42
  • Wonderful, Aretino! Thanks again! But then the second assert is false, right? –  Jun 05 '18 at 12:44

1 Answers1

0

For the first part please refer to my answer to the original question. I will repeat here the argument for the second case, but there must be an error in your question, because the locus of points such that $\gamma'^2=2\alpha'\beta'$ is the same ellipse as in the answer to the first part. This is obvious, because $\alpha'=(2/\sqrt3)\alpha$, $\beta'=(2/\sqrt3)\beta$, $\gamma'=(2/\sqrt3)\gamma$.

A circle is indeed the locus of $P$ when $\gamma'^2=\alpha'\beta'$. In this case it is easier to find the answer using cartesian orthogonal coordinates, with $x$ axis along side $AB$ of the triangle (see diagram below). For simplicity I also set $AB=AC=1$. Coordinates $(x,y)$ of point $P$ have a simple relation with $\alpha'$ and $\beta'$: $$ y={\sqrt3\over2}\alpha',\quad x=\beta'+{1\over2}\alpha' \quad\text{and}\quad \gamma'=1-\alpha'-\beta'\quad \text{by the given assumption.} $$ Plugging these into $\gamma'^2=\alpha'\beta'$ gives a simple equation for $P$: $$ (x-1)^2+\bigg(y-{1\over\sqrt3}\bigg)^2={1\over3}. $$ This is the equation of a circle with center $O=(1,1/\sqrt3)$ and radius $1/\sqrt3$.

enter image description here

Intelligenti pauca
  • 55,765
  • Bright as always, Aretino. To me, it seems then that the answer to the second question is "yes": but, what do you mean with "there must be an error in your question because in this case $\gamma^2<2\alpha\beta$?", I don't get this observation. –  Jun 05 '18 at 15:11
  • I think I got one thing. "Your" circle is tangent to the sides of the triangle in B and in C, while the diameter of "my" circle coincides with the side of the triangle. –  Jun 05 '18 at 15:16
  • The reference (for the second question) is this post: https://math.stackexchange.com/q/2808668/559615 –  Jun 05 '18 at 15:19
  • My proof was wrong, but the condition $\gamma^2=2\alpha\beta$ leads to an ellipse, not to a circle: I edited my answer to make that clear. The quantities $\alpha$, $\beta$, $\gamma$ in your subsequent question are not the same as the ones used here. – Intelligenti pauca Jun 05 '18 at 16:16
  • I see, and it is very intriguing! But my question is related to the case in which the side of the triangle coincides with the diameter of the circle (as in the original picture). In this case, what is the relation between $\alpha', \beta',\gamma'$? Is it still $\gamma'^2=2\alpha'\beta'$? In any case, thank you a lot for your nice reasoning! –  Jun 05 '18 at 17:09
  • You can reverse the argument above: start with the equation of the circle having $BC$ ad diameter: $$\left(x-{3\over4}\right)^2+\left(y-{\sqrt3\over4}\right)^2={1\over4}$$ and substitute $x$ and $y$ with the expressions given above in terms of $\alpha'$ and $\beta'$. The relation you'll find IS NOT $\gamma'^2=2\alpha'\beta'$. – Intelligenti pauca Jun 05 '18 at 17:19
  • The relation in that case can be written as $2\gamma'^2-\gamma'=2\alpha'\beta'$. – Intelligenti pauca Jun 05 '18 at 17:45