3

Say you have a row of 4 lights. Each light-bulb can be turned on/off independently. How many lighting combinations could you come up with?

enter image description here

My research:

Before asking this question I searched the forum to make sure this wasn't a duplicate. I found similar questions, but they had restrictions which I'm not imposing.

For example this question required that a number of lights always be left on, and this question imposed a lighting pattern.

I simply want to know without restrictions how many combinations there could be.

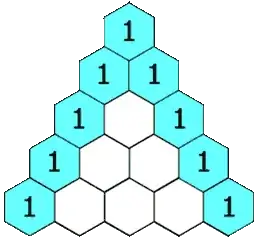
Reading the answers to the linked questions above I learned about Pascals triangle.

enter image description here

Studying the triangle it appeared to me that the number of combinations possible for N (the number of lights in a row) is the sum of all the numbers in the row of pascal's triangle that has the same amount of numbers as n+1.

For example if I had 1 light, there are 2 combinations, on or off.

Pascals second row (the number of lights + 1) the sum of that row adds up to 2. Thus representing the total number of combinations.

Is that correct, and if it is, is there a more formal algorithm to represent this sort of problem without having to draw out a pascal triangle for large data-sets?

YAHsaves
  • 143
  • 1
    Every light bulb can be turned on or off independently of the other ones. This gives you ${\text{on}, \text{off}} \times \dots \times { \text{on}, \text{off} } = 2^{d}$ choices where $d$ is any number of lightbulbs. – VHarisop Jun 01 '18 at 20:58
  • @VHarisop wow yes that is a simple way to think about it. Thank you! I see how Pascals triangle basically does the same thing in a more complex way. – YAHsaves Jun 01 '18 at 21:00
  • Since you introduced the Pascal triangle, it's worth mentionning that the sum of the $n$th row of this triangle is $2^n$ (the first row is the $0$th). See for instance https://math.stackexchange.com/questions/519832/proving-by-induction-that-sum-k-0nn-choose-k-2n – Jean-Claude Arbaut Jun 01 '18 at 21:01
  • Each element of a row in Pascal's triangle is added into two elements in the row below, which is one way to see that the sum doubles each time. – Joffan Jun 01 '18 at 21:12
  • Plenty of answers but here's another: think of it as a binary number. – badjohn Jun 01 '18 at 21:33
  • @badjohn that was actually why I asked the question! It was for a programing problem on a binary array. I don't know why I didn't think to just convert it to decimal and the outcome would be the same. – YAHsaves Jun 01 '18 at 21:41
  • @YAHsaves As a programmer, you should recognise a binary number. Think of each bulb as a bit and then the block of four is a nybble (one hex digit). – badjohn Jun 01 '18 at 21:45

3 Answers3

5

Each light has two positions and is independent of the others. By the multiplication principle there are $2^4=16$ possibilities. The row of Pascal's triangle that goes $1-4-6-4-1$ shows that there is one possibility with no lights on, four with one light on and so on. The sum is duly $16$

Ross Millikan
  • 383,099
3

What about saying that, since you have two possibilities for each light bulb, then you have $16(=2\times2\times2\times2)$ possibilities?

José Carlos Santos
  • 440,053
  • That seems easy enough! Thank you, very clear concise answer. I see how pascals triangle is basically doing the same thing but in a more complex way. – YAHsaves Jun 01 '18 at 20:59
1

The 'nth' row of Pascal's triangle has the coefficients for $(x+ y)^n$. Taking x= y= 1 the sum of those coefficients is $(1+ 1)^n= 2^n$.

user247327
  • 19,020
  • 2
  • 15
  • 21