What is the fourier transform of $e^{-\frac{t^2}2}$

Question

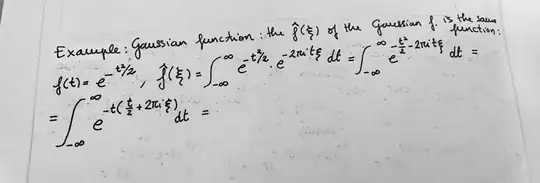
What is the fourier transform of $e^{-\frac{t^2}2}$. I need a classical solution, I mean, straight-forward. done by hand, without using tricks and convolutions. Many thanks in advance

First steps, am I on the right way?

Answer 1

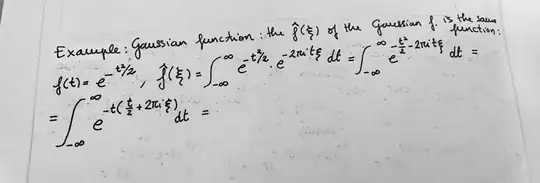
The solution involves completing the square in the exponent of the integrand, and then performing a $u$ substitution to get a well known integral that evaluates to 1:

$$\begin{align*}\mathscr{F}\left\{e^{-\frac{t^2}{2}}\right\}&= \int_{-\infty}^{\infty}e^{-\frac{t^2}{2}}e^{-2\pi i s t} dt\\ \\ &= \int_{-\infty}^{\infty}e^{-\frac{1}{2}(t^2+4\pi i st)} dt\\ \\ &= \int_{-\infty}^{\infty}e^{-\frac{1}{2}(t^2+4\pi i st-4\pi^2s^2)} e^{-2\pi^2s^2}dt\\ \\ &= \int_{-\infty}^{\infty}e^{-\frac{1}{2}(t+2\pi i s)^2} e^{-2\pi^2s^2}dt\\ \\ &= e^{-2\pi^2s^2} \int_{-\infty}^{\infty}e^{-\frac{\pi}{2}\left(\frac{t}{\sqrt{\pi}}+2\sqrt{\pi} i s\right)^2}dt\\ \\ &= e^{-2\pi^2s^2} \int_{-\infty}^{\infty}e^{-\pi\left(\frac{t}{\sqrt{2\pi}}+\sqrt{2\pi} i s\right)^2}dt\\ \\ &= {\sqrt{2\pi}}{e^{-2\pi^2s^2}} \int_{-\infty}^{\infty}e^{-\pi u^2}du\\ \\\ &= {\sqrt{2\pi}}{e^{-2\pi^2s^2}}\\ \\ &= {\sqrt{2\pi}} {e^{-\pi\left(\sqrt{2\pi}s\right)^2}}\\ \\ &= \mathscr{F}\left\{e^{-\pi\left(\frac{t}{\sqrt{2\pi}}\right)^2}\right\} \end{align*}$$