20

I've always wondered, what is the number of possible permutations of the Rubik's cube such that any two adjacent stickers has a different color. By a permutation I mean a configuration of the cube that can be achieved from the solved cube by only using the legal moves.

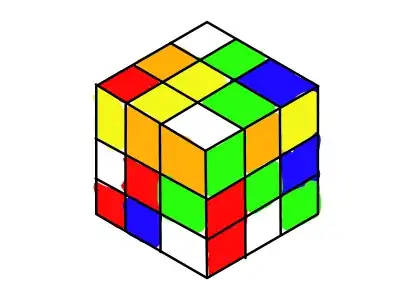
An obvious example is the superflip. This picture below is an example of a configuration which fails to fulfill the requirement.

enter image description here

I don't actually have any clue on how one might go about solving such a question and that's why I'm asking.

Extra question: This might be too vague question but it would be interesting to know if solving such cube as described above, takes more moves than one which has adjacent pieces with same color.

Mike Pierce
  • 19,406
Miksu
  • 1,394

1 Answers1

1

I decided to try solving this problem by a computer search. I wrote a Haskell program that basically assembles the Rubik's cube piece by piece while never placing two pieces next to each other in such a way that two adjacent stickers have the same colour. Finally, the program checks if the assembled cube is actually solvable by the standard moves. I got the program working, but I couldn't compute the final result, because it was taking too long. Instead, I tried calculating some kind of an estimate for the number of cubes with the desired property. The estimate I got is 224,223,685,920,000 solvable cubes. There are 43,252,003,274,489,856,000 solvable combinations in total, and the ratio is $$\frac{224,223,685,920,000}{43,252,003,274,489,856,000}=5.184\times 10^{-6}.$$ The code can be found on github along with an in-depth explanation of the maths and implementation.

Miksu
  • 1,394