Finding complete sufficient statistic

Asked May 18 '18 at 00:08

Active May 18 '18 at 00:08

Viewed 307 times

let $X_1 , ....,X_n$ be iid. $Uniform[-\theta,\theta]$. I need to find the complete sufficient statistic.

I know that $T=(X_{(1)}, X_{(n)} )$ is a sufficient statistic for $\theta$.Also i know T is not a complete sufficient statistic.

I want to prove it. So first I tried to use the Basu's theorem . But in this case $R = X_{(n)} -X_{(1)}, $ is not a ancillary statistic.

So i tried prove using the definition of the complete sufficient statistic.

Here i have attached my work so far.

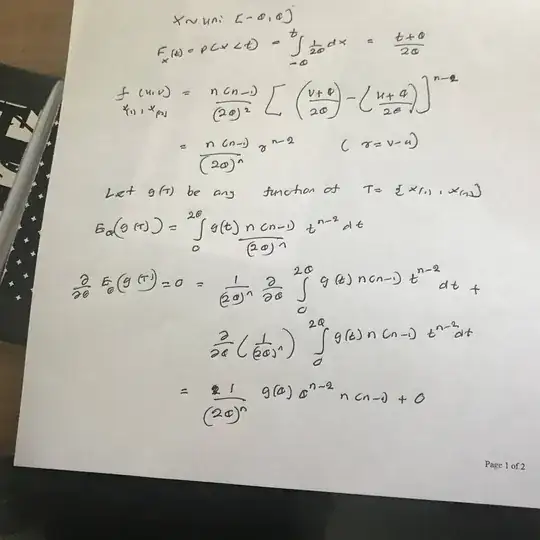
But by doing like this , seems like that i am going to prove that T is a complete sufficient statistic.

So can someone help to figure it out what i did incorrectly ?

Thank you

asked May 18 '18 at 00:08

student_R123

See here: https://stats.stackexchange.com/questions/225580/jointly-complete-sufficient-statistics-uniforma-b – Math1000 May 18 '18 at 00:24
@Math1000 Hi in that question they are trying to prove that T is a complete sufficient statistic. But as far as i know, it is not. – student_R123 May 18 '18 at 00:29
What about $X_{(n)} + X_{(1)}$? – spaceisdarkgreen May 18 '18 at 03:35
@spaceisdarkgreen Thank you for the hint. I will try that. – student_R123 May 18 '18 at 03:39
$|X_1|,\cdots,|X_n|$ is i.i.d. and $U(0,\theta)$ distributed. $\max_{1\le i\le n}|X_i|$ is the complete sufficient statistic. – JGWang May 19 '18 at 03:46
Asked and answered at https://stats.stackexchange.com/q/346883/119261. – StubbornAtom Jun 28 '20 at 17:41

0 Answers0