How do I represent the set of all finite bit strings?

Question

At first I thought I could just represent them with the set of natural numbers, because each bit string represents some natural number. However doing this would mean the strings '010' and '00010' are the same, which they are not.

Answer 1

Here's one easy way to biject the finite binary strings to the natural numbers (let's say we're thinking of the natural numbers as not including zero):

• Step $1$: put a "$1$" on the left.

• Step $2$: view the resulting string as a number in binary as usual.

E.g. "$010$" turns into "$1010$," which is ten. The empty string meanwhile turns into the string $1$, which then turns into the number one.

---

If we want to get $0$ in the mix too, we can just add "Step $3$: subtract $1$" to the above.

Answer 2

(this answer is a Wiki, you can edit and improve it!)

The non-numerical nature of bit string calls for contextualization. There are some alternative ways, in pure Mathematics, to do both:

• Bit string definition, and
• Define the Set X of All Finite Bit Strings.

PS: as commented by @NoahSchweber, the "standard name" of $X$ in Mathematical Logic, is $2^{<\omega}$.

Defining bit string

In Computation bits (binary digits) are not numbers, are "raw symbols", typically 0 and 1.

A bit string s is a sequence of zero or more bits. For example 010 and 00010 are distinct elements of $X$. In particular s=``, the empty string, is an element of $X$.

We can cast to numbers of the domain $D=\{0,1\}$ using sequences:
  ``≡(); 0≡(0); 1≡(1); 00010≡(0,0,0,1,0).

Bit strings are equipped with the concatenation operation. If a and b are bit strings, then the concatenation $c=a||b$ is also a bit string.

PS: the empty string is important because it is the neutral element of the concatenation.

Defining X by Kleene star

As commented by @Phicar, the easiest way to define a bit string is using the Kleene star:
 $\{0,1\}^*$

It is a "generator expression", producing elements by concatenation, with lengths ranging from zero to countably infinite. Thus, it is not explicit regarding finiteness, as requested.

Back to the Kleene star definition:
  $X = \bigcup _{k \in \mathbb{N}}\{0,1\}^k ~ \equiv ~ \{0,1\}^*$

We can be more explicit, limiting k to the length of the "finite bit strings": \begin{equation} X_k = \bigcup _{i = 0}^{k}\{0,1\}^i \end{equation}

This definition seems the requested answer.

Note. We can rewrite it using recursion, to emphasize the hierarchy in k:
  $X_{k} = \{0,1\}^k \cup X_{k-1}$

---

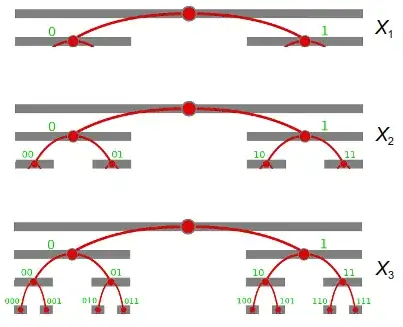
NOTES, EXAMPLES AND ILLUSTRATIONS

Examples of $\{0,1\}^i$, the generator of all bit strings with length i:

$\{0,1\}^0$ = {``}
$\{0,1\}^1$ = {0,1}
$\{0,1\}^2$ = {00,01,10,11}

Examples of $X_k$, the set of all bit strings with no more than k bits, with respective cardinalities:

X₀ = {``};   $|X_0|=1$.

X₁ = {``, 0, 1};   $|X_1|=3$.

X₂ = {``, 0, 00, 01, 1, 10, 11};   $|X_2|=7$.

X₃ = {``, 0, 00, 000, 001, 01, 010, 011, 1, 10, 100, 101, 11, 110, 111};   $|X_3|=15$.

  Note. The sequence of cardinalities (1,3,7,15,...) is A000225.

Pictorial view of the hierarchical structure suggested by the recurrent definition. it can be associated with the Cantor Set picture and the binary tree:

Notes about cardinality:

For fixed length bit strings, $|S_k|=2^k$, so $|X_k|=2^k+|X_{k-1}|$. Then, by induction:

  $|X_k|=2^{k+1}-1$.

---

Comments under discussion:

As the curious cardinality of Cantor Set, the value of $|X_{\infty}|$ seems uncountable.

Using the bijection of the @NoahSchweber's answer, we can say that the (countable) infinity of the cardinality of Natural numbers overflows by 1 bit (to the uncountable infinity of Cantor Set).

Answer 3

I am late to this question but, since it appeared in my feed, the most obvious way to represent all of the finite bit strings is as functions on the natural numbers that are zero, almost everywhere.