0

Based on Why do differentiating and integrating 'work'?

In differentiation, you take the gradient of a point $x$ by differentiating. To this, you take two points on the graph, one which is the point where you want to find the gradient of, and another one (which is explained later).

Differentiation

As you can see, there are two points:

$$(a,f(a)) \text{ and } (a+h,f(a+h))$$

Where $h$ is the distance between the points.

We take the gradient of these two points, and we get:

$$f'(x)=\dfrac{f(a+h)-f(a)}{(a+h)-a}$$

$$=\dfrac{f(a+h)-f(a)}{h}$$

To find the gradient of a point, we take $h$ as $h \rightarrow 0$ which gives us the gradient of the graph at $x$

So, now about integration.

integration

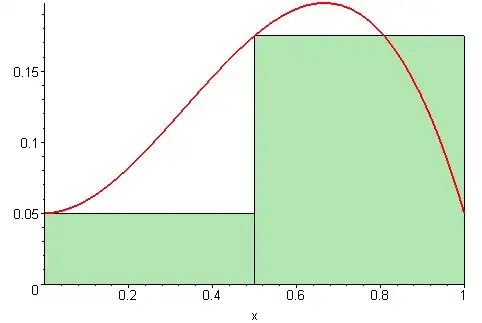
I understand that integration is using a trapezium rule to take the limit as the width of each strip $\rightarrow 0$ and the number of strips $\rightarrow \infty$

This gives us $$ \lim\limits_{n\to\infty} \sum\limits_{i=1}^n f(x_i)\Delta x_i$$

$n=$ number of strips

$\Delta x_i =$ width of strip $i$

So what is the algebraic reasoning behind this transformation of a function?

All images belong to Source

Xii
  • 2,149
  • What exactly do you mean by "algebraic reasoning"? – Exit path May 02 '18 at 15:48
  • @leibnewtz $$f'(x)=\dfrac{f(a+h)-f(a)}{(a+h)-a}=\dfrac{f(a+h)-f(a)}{h}$$ The integrating equivalent – Xii May 02 '18 at 15:49
  • The direct equivalent is just the definition of the Riemann sum. The geometric equivalent is that you approximate the area under the curve by the area of a bunch of rectangles that lie under (or mostly under) the curve. As you make the rectangles narrower, the white space and "black space" (i.e. rectangle area above the curve) get smaller. Thus for the derivative, you approximate the slope at a point using the slope of a line between two points that are actually on the given curve. For the integral, you approximate the area as the area under a "curve" close to the given curve. – Ian May 02 '18 at 15:54
  • This is a pretty good summary of calculus, but it's not clear what you are asking. Are you wanting an algebraic motivation that's completely divorced from geometry? – Jair Taylor May 02 '18 at 16:08
  • @VortexYT Why should the two ideas be defined similarly? One is the limit of a function, the other is the limit of a sequence. That the two are connected by the fundamental theorem of calculus is pretty amazing – Exit path May 02 '18 at 16:13
  • If you want to really understand the link between differentiation and integration, it is best that you have a look at the proof of Fundamental Theorem of Calculus. For me a proof is only thing that explains the mystery. Any other tactics only reduce the mystery somewhat and sometimes lead to the wrong path. – Paramanand Singh May 03 '18 at 03:15

2 Answers2

1

Not sure if this answers your question, but this is how I like to think about integration. enter image description here

Consider a small change of the area under $f(x)$, this is $dA$. Since $dA$ is small, the red part (change in area) approaches roughly $f(x)dx$ (area of rectangle), so $dA=f(x)dx$, or $$\frac{dA}{dx}=f(x)$$

This means that $A(x)$ is the anti-derivative of $f(x)$.

cansomeonehelpmeout
  • 14,020
  • 3
  • 29
  • 55
0

We can estimate differentiation by taking the two points $f(x)$ and $f(x+h)$ like you said, and then shrinking $h$. What algebraic differentiation does is reduces the $h$ to an extremely small quantity, and outputs the gradient between two points that are virtually the same but only just not.

With the Trapezium Rule for Integration Approximation, you have a class width ($h$ or $w$). As your h shrinks, the values get closer. Again, all algebraic integration does is shrink your h to an extremely small quantity and gives you the area there, which due to the tiny class width, is accurate to the curve.

Rhys Hughes
  • 13,103