First of all, I see that this appears to be a duplicate of this but please tell me where my solution guide appears to be wrong.
A man and a woman decide to meet at a certain location. If each of them independently arrives at a time uniformly distributed between 12 noon and 1PM, find the probability that the first to arrive has to wait longer than 10 minutes. (Hint: Denote by $X$ and $Y$ the time past 12 noon that the man and woman arrive. Then you have to compute $P(X+10<Y) + P(Y+10<X)$, which by symmetry equals $2P(X+10<Y)$. So basically you have to compute $P(X+10<Y)$. To do this, you will have to compute a double integral. When you do that, be very careful with the limits of that integral so that you integrate the distribution function only over those values of $x$ and $y$ such that $x+10<y$.
My first step was to write out the pdf of $x$ and $y$
$f(x)=\frac{1}{60}$ where $0\le x \le 60$
$f(y)=\frac{1}{60}$ where $0\le y \le 60$
Because they're independent the joint is just $f(x,y)=f(x)f(y)=\frac{1}{3600}$
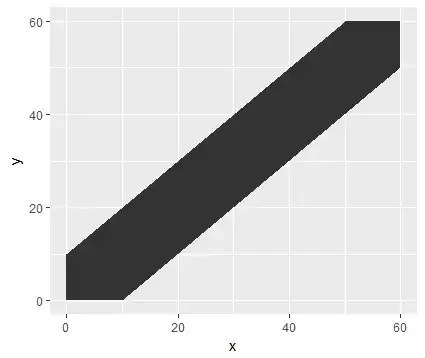
I drew a graph to try to figure out the limits of integration...
From the picture I surmised that the answer is just the area of the polygon in the middle divided by 3600 which makes sense because the area of the box is 3600 and 3600 over 3600 is 1 which is what we want out of a pdf. Anyway the answer using that method is just $3600-\frac{1}{2}50*50-\frac{1}{2}50*50=1100$ and $1100/3600=11/36$ which is the same answer from the linked problem. However, I have to do the problem as a double integral and I can't figure out what my limits of integration should be. Assuming the easy way is correct, that would make my solution guide incorrect. Here's what it says...
$$ \begin{align} P(X + 10 < Y) &= \int_{10}^{60}\left[\int_0^{y-10}\frac{1}{3600}dx \right]dy\tag1\\ &= \frac{1}{3600}\int_{10}^{60}\left[\int_0^{y-10}dx \right]dy\tag2\\ &= \frac{1}{3600}\int_{10}^{60}\left[y-10\right]dy\tag3\\ &= \frac{1}{3600}\left[\frac{y^2}{2}-10y\right]_{10}^{60}\tag4\\ &= \frac{25}{72}\tag5\\ \text{since we want 2x of the above probability}\\ 2*\frac{25}{72}&=\frac{25}{36} \end{align} $$
So my follow up questions are, what should the limits of integration be to do this with a double integral and what do the limits of integration used above actually give us or what question is my solution guide giving the answer to?