Finding a probability given two random variables

Question

[Original at https://i.sstatic.net/0g15I.png]

The time until failure, T, of a product is modeled by a uniform distribution on $[0, 10]$. An extended warranty pays a benefit of $100$ if failure occurs between time $t = 1.5$ and $t = 8$.

The present value, $W$, of this benefit is

$$ W = \left\{ \begin{array}{cc} 0, & 0 \leq T < 1.5, \\ 100e^{-0.04T}, & 1.5 \leq T < 8, \\ 0, & 8 \leq T \leq 10. \end{array} \right. $$

Calculate $P(W < 79)$.

This problem we were doing in class and the argument was as follows

$$ P(W<79) = P(W < 79 | 0 \leq T < 1.5) P(T < 1.5) + P(W < 79 | 1.5 \leq T < 8)P(1.5 \leq T <8 ) + P(W<79| 8 \leq T \leq 10 ) P(8 \leq T \leq 10 ) $$

MY question is, why do we have to break in such a cases? This was done by using the law of total probability?

Secondly, can we say

$$ P(W < 79 | 0 \leq T < 1.5) P(T < 1.5) = 0 $$

since $W = 0 $ on this interval of $T$ ? Because when trying to compute this I get

$$ P(W < 79 | 0 \leq T < 1.5) P(T < 1.5) = P( \{W < 79 \} \cap\{0 \leq T \leq 1.5 \} ) =0 $$

Answer 1

Yes to the last question. And, no, you don't have to do this precisely this way, but it does spell everything out nicely. The practical way to do this if you already understand probability distributions is to solve $79=100e^{-0.04T}$ for T, getting 5.89. Then your answer is 1-[(5.89-1.5)/10], or a 56.1% chance of paying less than 79 dollars in present value.

Answer 2

It is the formula of addition for independent events: $$P\left((W<79)\cap (T_1\cup T_2\cup T_3)\right)=\\ P\left([(W<79)\cap T_1]\cup [(W<79)\cap T_2]\cup [(W<79)\cap T_3]\right)=\\ P((W<79)\cap T_1)+P((W<79)\cap T_2)+P((W<79)\cap T_3).$$ Note: $$\underbrace{P(W < 79 | 0 \leq T < 1.5)}_{=1} P(T < 1.5) = P( \underbrace{\{W < 79 \} \cap\{0 \leq T \leq 1.5 \}}_{=\{0 \leq T \leq 1.5 \}} ) =\frac{1.5}{10}=0.15.$$ The easier way to calculate: $$P(W<79)=1-P(W>79)=\\ 1-[\underbrace{P((W>79) \cap (0\le T<1.5))}_{=0}+P((W>79) \cap (1.5\le T<8))+\underbrace{P((W>79) \cap (8\le T\le 10))}_{=0}]=\\ 1-P((W>79) \cap (1.5\le T<8))=\\ 1-P(1.5\le T<5.89)=1-\frac{5.98-1.5}{10}=0.561.$$

Answer 3

I don't really like using conditional probability. I prefer indicator variables or partitions. I totally get your confusion and hope that I have understood your confusion as well.

Firstly, let's partition $\Omega$ by using $T$, i.e. let's identify the kinds of events in terms $T$: For any $\omega \in \Omega$, we must have $\omega$ be in exactly one of the following cases:

$$1.) \ 0 \le T<1.5$$ $$2.) \ 1.5 \le T<8$$ $$3.) \ 8 \le T<10$$

Why do we do this instead of something like $T\in[0,1], T\in[1,2], ..., T\in[9,10]$? This is because the way the range of $W$ is partitioned. It may be helpful to write $W$ as follows:

$$W = 0 \times 1_{0 \le T<1.5} + 100e^{-0.04T} \times 1_{1.5 \leq T < 8} + 0 \times 1_{8 \le T<10}$$

Going back to the cases, let's name them, respectively, as $B_1$, $B_2$ and $B_3$. If we also name $A := \{W<79\}$, then we have

$$P(A) = P(A \cap B_1) + P(A \cap B_2) + P(A \cap B_3)$$

Why? Here's a fancy drawing:

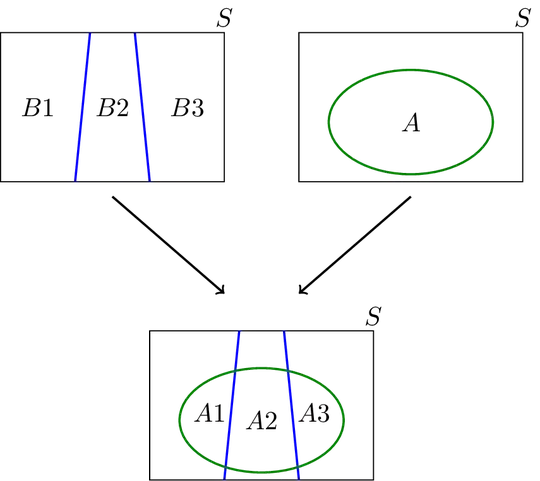
This is actually an extension of $P(A) = P(A \cap B) + P(A \cap B^c)$ known as, as you pointed out, the law of total probability, except I use the version that doesn't have conditional probability.

Thus, $W$ can be written as follows:

$$W = 0 \times 1_{B_1} + 100e^{-0.04T} \times 1_{B_2} + 0 \times 1_{B_3}$$

Now let's compute $P(A \cap B_1)$ and $P(A \cap B_3)$ by examining $A \cap B_1$ and $A \cap B_3$. Firstly, for $A \cap B_1$

$$A \cap B_1 = \{\omega | \{W(\omega) < 0.79\} \cap \{ 0 \le T(\omega) < 1.5 \}\}$$

We want to compute the probability of all the sample points $\omega$ satisfying both cases, i.e. sample points in both sets $A := \{W < 79\}$ and $B_1 := \{ 0 \le T < 1.5 \}$. Now if $\omega \in B_1$, then $\omega \notin B_2, \notin B_3$ by the very definition of partitions. Thus, for such an $\omega \in B_1$, i.e. $0 \le T(\omega) < 1.5$, this is what becomes of $W$ for this particular $\omega$:

$$W(\omega) = 0 \times 1_{B_1}(\omega) + 100e^{-0.04T(\omega)} \times 1_{B_2}(\omega) + 0 \times 1_{B_3}(\omega)$$

$$ = 0 \times 1 + 100e^{-0.04T(\omega)} \times 0 + 0 \times 0$$

$$ = 0 + 0 + 0 = 0$$

For this $\omega$ that is said to also in be $A$, i.e. $W(\omega) < 79$, we now have that $W(\omega) = 0 < 79$. This statement is always true. Hence for $\omega \in B_1$, $\{W < 79\} = \{0 < 79\} = \Omega$, i.e.

$$A \cap B_1 = \Omega \cap B_1 = B_1$$

It is not that $A = \Omega$ but rather when $A$ is intersected with $B_1$, $A$ might as well have been $\Omega$. This is because as it turns out $B_1 \subseteq A$, i.e. $$\{0 \le T < 1.5\} \subseteq \{W < 79\}$$

Thus, $$P(A \cap B_1) = P(B_1)$$ $$\to P(A) = P(A \cap B_1) + P(A \cap B_2) + P(A \cap B_3) = P(B_1) + P(A \cap B_2) + P(A \cap B_3)$$

Similarly, $$P(A \cap B_3) = P(B_3)$$

Thus, $$P(A) = P(B_1) + P(A \cap B_2) + P(A \cap B_3) = P(B_1) + P(A \cap B_2) + P(B_3)$$

Finally, let's examine $A \cap B_2$.

$$A \cap B_2 = \{\omega | \{W(\omega) < 79\} \cap \{ 1.5 \le T(\omega) < 8 \}\} = \{\omega | \{100e^{-0.04T(\omega)}1_{B_2} < 79\} \cap \{ 1.5 \le T(\omega) < 8 \}$$

$$= \{\omega | \{100e^{-0.04T(\omega)}1_{ 1.5 \le T(\omega) < 8 } < 79\} \cap \{ 1.5 \le T(\omega) < 8 \}\}$$

$$= \{\omega | \{100e^{-0.04T(\omega)} < 79\} \cap \{ 1.5 \le T(\omega) < 8 \}\}$$

$$= \{\omega | \{T(\omega) > \frac{\ln(0.79)}{-0.04}\} \cap \{ 1.5 \le T(\omega) < 8 \}\}$$

$$= \{\omega | \{8 > T(\omega) > \frac{\ln(0.79)}{-0.04} \}\}$$

Luckily, $A$ and $B_2$ were 'related' so they intersect nicely enough such that computing $P(A \cap B_2)$ is now simply a matter of computing the probability that $T$ falls in the interval $(\frac{\ln(0.79)}{-0.04},8)$

Therefore,

$$P(A) = P(0 \le T<1.5) + P(8 > T > \frac{\ln(0.79)}{-0.04}) + P(8 \le T<10)$$

Compare:

$$1 = P(\Omega) = P(0 \le T<1.5) + P(8 > T \ge 1.5) + P(8 \le T<10)$$

What do we learn from the comparison? It seems that the event $A$ is pretty big, i.e. $W<79$ with high probability. After all, it covers the entire range of $T$, which is $[0,10]$ except $(1.5,\frac{\ln(0.79)}{-0.04})]$. That makes sense since $W$ is $0$ for $\frac{(10-8) + (1.5-0)}{10-0} = 35$% of a uniformly distributed range.

Actually, we may compute

$$P(A) = 1 - P(1.5 \ge T < \frac{\ln(0.79)}{-0.04})) \approx 56.069 \ \text{%}$$