5

Today I learned that the two branches of the standard hyperbola $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ have no common tangents, but have only one common normal ($y=0$). So I wondered if if it has more than one common normal as well.

I began by taking two parametric points $P(\theta_1)$ and $Q(\theta_2)$. We know that a general slope of normal is given by: $-\frac ab\sin\theta$. Setting slope on both points equal we get: $\sin\theta_1=\sin\theta_2$. This implies either $\theta_1=\theta_2=0$ (a case which we already covered) or $\theta_1+\theta_2=\pi$.

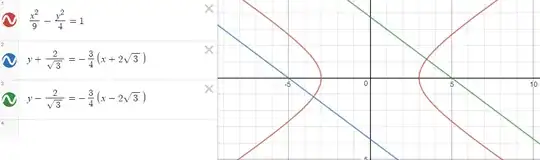
However, a quick desmos graph shows that the normals I've calculated are instead parallel and non-intersecting: (for $\theta_1=30^\circ$ and $\theta_2=150^\circ$)

enter image description here

So, is it true that the two branches of a hyperbola have not more than one common normal? Or did I miss some calculation in my step?

Gaurang Tandon
  • 6,665
  • It's true, and you can figure this intuitively too. If you try drawing perpendicular lines to the curve, it'll either not intersect or intersect at an odd angle. It is only at the very hump that the curve is normal to itself. – Christopher Marley Apr 24 '18 at 02:31
  • @ChristopherMarley Thanks for your feedback! I was trying to go for a more formal proof, but yes, I think we can see this intuitively as well. – Gaurang Tandon Apr 24 '18 at 02:35

3 Answers3

3

Intuitive: take a point $P$ on the left piece, below the horizontal. Take the normal to that branch at that point. It will point downwards, so if it intersects the right piece, it will be a point lower $P'$. Now take the normal to the right piece at that point $P'$. It will go lower from right to left. So if it intersects the left piece, it will be at a point $P''$ lower than $P'$, and so lower than $P$, so cannot get back to $P$.

In general, if we have two convex closed regions with smooth boundary that are disjoint then they have have a common normal $AB$. Indeed, we can consider points $A$, $B$ in each of the regions that are closest. Assume moreover that the line $AB$ intersects the each region along a half line and at least one of the region is strictly convex. Then $AB$ is the only common normal. The proof is the same.

orangeskid
  • 56,630
2

What you’ve done so far is correct, but incomplete. So far you’ve found pairs of points for which the normals to the hyperbolas have the same slope, but you haven’t shown that the normals at these points coincide.

This suggests another way to search for common normals: look for points $P$ and $Q$ on the hyperbola for which the line through them is also the normal at both points.

amd
  • 55,082
0

Two normals erected in points of the same branch are not even parallel. Two normals erected in points $P_{\rm left}$ and $P_{\rm right}$ on different sides of the $y$-axis intersect the $x$-axis in two different points $x_{\rm left}<-a$ and $x_{\rm right}>a$, except the common normal $y=0$.

Christian Blatter
  • 232,144