4

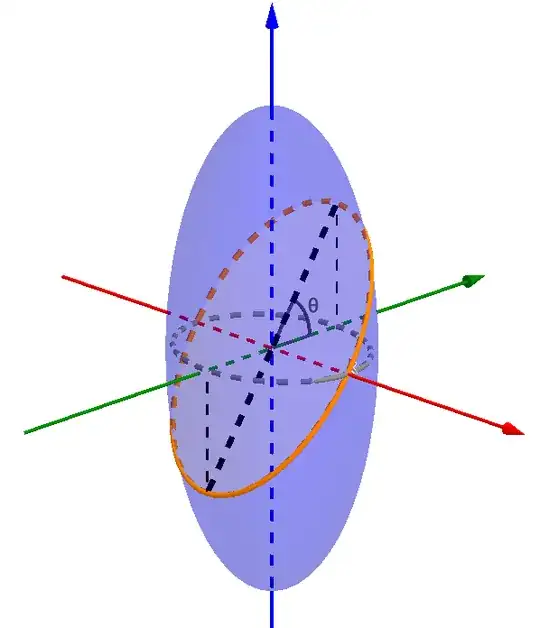
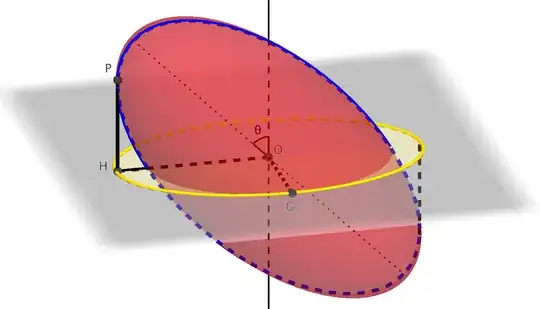
I currently have an assignment in which I have to model the drag forces acting on a rugby ball as it rotates through the air. One of the variables in the drag force equation is the cross section of the shape relative to the direction of motion.

I have assumed the shape of the football to be a prolate spheroid with a minor axes 'a,a' and a major axis 'c'. If rotating in one direction, I imagine it would be calculated by finding the radius of the spheroid at a given rotation using the formula $$ r = \sqrt{\frac{a^2c^2}{c^2cos^2(\theta)+a^2sin^2(\theta)}} $$ I am confused as to how this would translate into rotation on more than one axis.

Can anyone can link me to a resource that explains this concept? I have scoured google but haven't found any literature on this specific topic.

Thanks in advance.

EDIT: The intersecting plane passes through the center of the spheroid.

James Storey
  • 43

1 Answers1

2

If what you need is the intersection between your spheroid and a plane $\alpha$ passing through its center (your question is not clear), then the answer is quite easy.

First of all, due to symmetry, the only angle that matters is that between the major axis of the spheroid and the normal to $\alpha$: let's call it $\theta$. With a suitable choice of coordinates, the equation of the spheroid can be written as: $$ {x^2\over a^2}+{y^2\over a^2}+{z^2\over c^2}=1 $$ and the equation of plane $\alpha$ is: $$ z=y\tan\theta. $$ Combining these equations we can eliminate $z$ to get $$ {x^2\over a^2}+{y^2\over b^2}=1, \quad\hbox{where:}\quad b^2={a^2c^2\over a^2\tan^2\theta+c^2}. $$ The intersection between the spheroid and $\alpha$ is an ellipse, the above equation representing its projection on the $xy$ plane. One of the semi-axes has length $a$ both for the ellipse and its projection, while the other one is tilted of an angle $\theta$ with respect to the $xy$ plane and its length is thus $$ b'={b\over\cos\theta}={ac\over\sqrt{a^2\sin^2\theta+c^2\cos^2\theta}}. $$

enter image description here

EDIT.

If you are looking, instead, for the projection of the spheroid onto a plane, then it is still an ellipse (see diagram below) whose semi-axes are

$$ OG=a,\quad OH=\sqrt{a^2\cos^2\theta+c^2\sin^2\theta}. $$

enter image description here

Intelligenti pauca
  • 55,765