7

Consider the function $$f(x)=\prod_{n=0}^\infty\operatorname{sinc}\left(\frac{\pi \, x}{2^n}\right),\tag1$$ where $\operatorname{sinc}(z)$ denotes the sinc function. It arises as a Fourier transform of the Rvachev $\operatorname{up}(x)$ function, which is basically a shifted version of the Fabius function (see, for example $^{[1]}$$\!^{[2]}$$\!^{[3]}$). Curiously, if we take a finite partial product from $(1)$ with at least 2 terms, its Fourier transform will be a continuous piecewise-polynomial function with finite support (and with continuous derivatives of progressively higher orders as we include more terms).

We restrict our attention only to $x\ge0$. The function $f(x)$ has zeros at positive integers, and oscillates with a quickly decaying amplitude. Its signs on the intervals between consecutive zeros follow the same pattern as the Thue–Morse sequence. 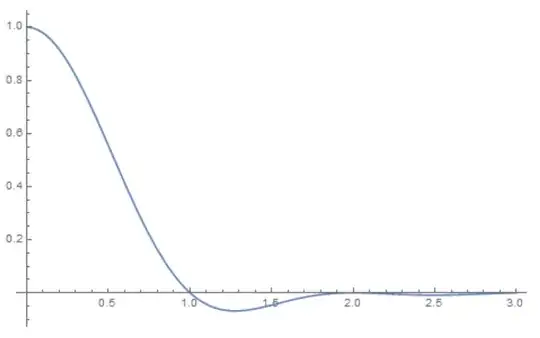graph of f(x) It appears that $f(x)$ has exactly one extremum on each interval between consecutive zeros (minimum or maximum, depending on its sign on that interval) — but I have not been able to find a complete rigorous proof of it. Can you propose one?

Update: I extracted the second part of my original question into a separate one and edited it significantly. The following is just an interesting observation:

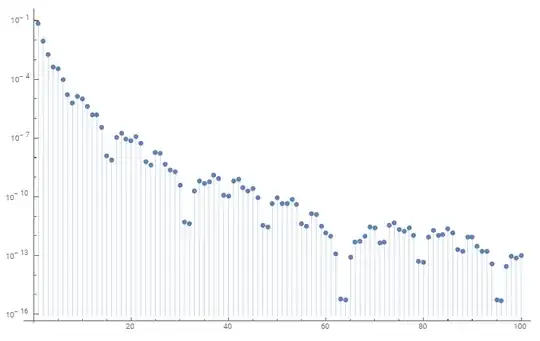
Let us denote the value of the extremum on the interval $n<x<n+1$ as $\epsilon_n$. The absolute values of the extrema $|\epsilon_n|$ generally tend to decrease as $n$ increases, but they do not decrease strictly monotonically and, in fact, show quite irregular behavior, sometimes increasing sporadically. Here is how their graph looks on log scale: absolute values of the extrema

Vladimir Reshetnikov
  • 32,650

1 Answers1

8

About the first question, an idea might be to use the Weierstrass product

$$\text{sinc}\left(\frac{\pi z}{2^n}\right)=\prod_{m\geq 1}\left(1-\frac{z^2}{(2^n m)^2}\right)$$ such that $$ f(z)=\prod_{n\geq 0}\text{sinc}\left(\frac{\pi z}{2^n}\right)=\prod_{m\geq 1}\left(1-\frac{z^2}{m^2}\right)^{\nu_2(m)+1} $$

$$ f'(z) = -2z\left(\sum_{m\geq 1}\frac{\nu_2(m)+1}{m^2-z^2}\right)\prod_{m\geq 1}\left(1-\frac{z^2}{m^2}\right)^{\nu_2(m)+1}.$$ The term $-\sum_{m\geq 1}\frac{\nu_2(m)+1}{m^2-z^2}$ has a simple pole with a positive residue at each $m\in\mathbb{N}^+$. In particular such function is increasing on the connected components of its domain $\cap \mathbb{R}^+$ and there cannot be more than one stationary point for $f$ between two consecutive zeroes.

The presence of the mildly erratic function $\nu_2$ also explains the apparent irregularity in the distribution of the stationary values for $f$. On the other hand by the previous formula for $f'$ (which essentially is a rephrasing of the Gauss-Lucas theorem) it is reasonable to expect that the stationary points converge to the midpoints of the intervals defined by the zeroes of $f$, hence an estimation for the decay of the stationary values can be performed by summation by parts, considering the average values of $\nu_2$ over larger and larger intervals.

Jack D'Aurizio
  • 361,689