1

For context this question is slightly related to this question on parameter paths for fractal animations

Most fractals I know about iterate some function and then output a color which is a function of some decision. For example Mandelbrot and Julia fractals outputs a color which is a function of the number of iterations $i$ where binary decision $|z_i|>k$ first (the lowest such $i$) gets triggered.

Can we build fractals which instead are functions of discrete sums or integrals?

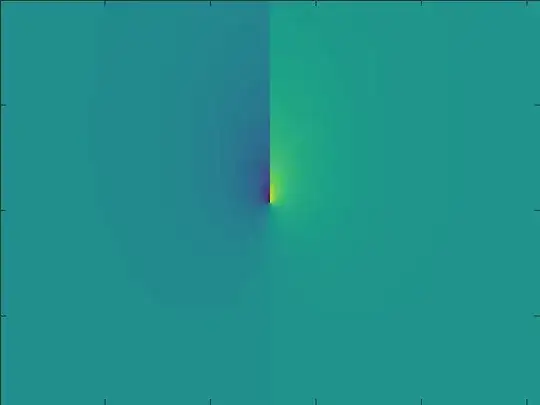
I made an attempt here with iteration $$z_t =c+{(z_{t-1})}^{t\alpha}$$ and sum / integral: $$I = \sum_{i=0}^{32} \exp(-|z_t|^{1/2})\arg(z_t)$$

For one fixed value of $\alpha$ this gives us a function $\mathbb C\to \mathbb R$. Here is an animation on $$\mathcal R \in [-1/2,1/2], \mathcal I\in[-1/3,1/3] \text{ for } \alpha \in [1,1.5]$$ (Many thanks to user @Peter Taylor who showed me how to get this animation format working.) $\alpha$

So to the question I am looking for other fractals of the same kind: being possible to express as functions involving integrals / sums of iterated self references. Any reference or homemade one is welcome.

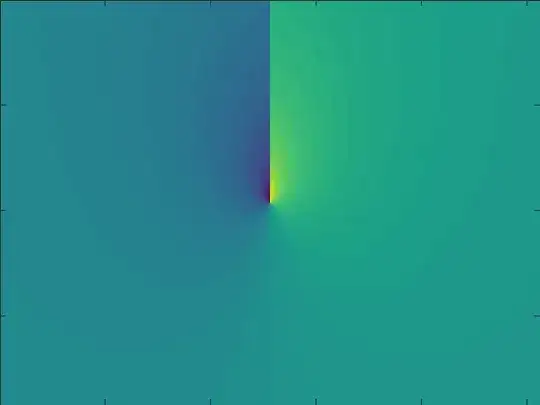
Here is last term only, as requested by @Rahul :

mathreadler
  • 26,534
  • Not an answer, but have you tried drawing just the last term in your sum, i.e. $\exp(-|z_{32}|^{1/2})\arg(z_{32})$? I'm curious whether most of the fractal nature of the plot is coming from the later terms, and the early ones are just serving to reduce the contrast. –  Apr 17 '18 at 15:03
  • @Rahul you may be right, I have not checked it. I first thought the lack of contrast was dependent on the exponent in the exp, but I have not tried very many of those either. – mathreadler Apr 17 '18 at 15:28

0 Answers0