10

(it is a follow-up on my previous question)

Let's define $t_n$ by the recurrence $$t_0 = 1, \quad t_n = (-1)^n \, t_{\lfloor n/2\rfloor}.\tag1$$ It is easy to see that $|t_n|=1$, and the signs follow the same pattern as the Thue–Morse sequence: $$1,\,-1,\,-1,\,1,\,-1,\,1,\,1,\,-1,\,-1,\,1,\,1,\,-1,\,1,\,-1,\,-1,\,1,\,...\tag2$$ (see this question for an example of a non-recursive formula for $t_n$).

Now, let: $$\mathcal{L}(z)=\lim_{n\to\infty}\,\sum_{k=1}^{2^n-1}t_k\,k^z.\tag3$$ I conjecture that the following propositions hold:

$\color{gray}{\text{(a)}}$ The limit $\mathcal{L}(z)$ exists for all $z\in\mathbb C$.

$\color{gray}{\text{(b)}}$ $\mathcal{L}(z)$ is an entire function of $z$.

$\color{gray}{\text{(c)}}$ $\mathcal{L}(z)=0$ if and only if $z\in\mathbb Z^+$.

Can we prove these conjectures? Can we find a different representation of $\mathcal{L}(z)$? Does this function have any interesting properties?

Update: The "if" part of the conjecture $\color{gray}{\text{(c)}}$ is certainly true. I am now pretty sure the "only if" part fails at some points on the imaginary axis (e.g. near $z\approx i\,4.53236...$; is it exactly $i\,\pi/\ln2$?). I am still wondering if there are any zeros except positive integers and off the imaginary axis.

Update: I found a very relevant and interesting paper (preprint) by Giedrius Alkauskas, Dirichlet series associated with Thue–Morse sequence$^{[1]}$$\!^{[2]}$ (be aware that the author claims$^{[3]}$ some results in it may be incorrect).

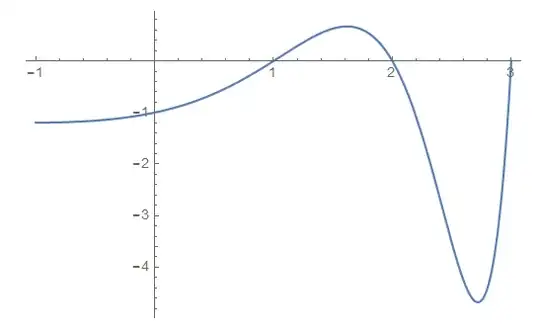
Here is my attempt to plot the function for a range of real arguments: the function plot

Community
  • 1
Vladimir Reshetnikov
  • 32,650
  • 1
    here a form i figured in thue-morse sequence, I hope it's relevant for your quest. – Abr001am Apr 06 '18 at 06:17
  • 3
    A bit of plotting with Mathematica suggests that $z_k=(2k+1)\pi i/\ln 2, k=0,1,2,\ldots,$ might all be zeros. I truncated the sum at $k=255$, so I won't bet any money on it, but so far that is suggested. – Jyrki Lahtonen Apr 06 '18 at 20:27
  • Perhaps, a more natural function to ask about would be $\displaystyle\lim_{n\to\infty}\sum_{k=0}^{2^n-1}t_k,\left(2k+1\right)^z$. – Vladimir Reshetnikov Apr 08 '18 at 01:08
  • @VladimirReshetnikov It's just $(2^z-1)\mathcal{L}(z)$ - what's so special about it? BTW, the statement on zeros mentioned by Jyrki Lahtonen is proven correctly in the paper you've found (worth noting in the text of the question, nothing more). – metamorphy Apr 08 '18 at 18:37
  • Right, there is not a significant difference. I just meant that if we start summation from $k=0$ (because we do not have to care about $0^z$ for negative $z$), then there is exactly $2^n$ terms. – Vladimir Reshetnikov Apr 09 '18 at 01:21
  • 1
    Another related paper: http://algo.inria.fr/seminars/sem92-93/allouche.pdf – Vladimir Reshetnikov Apr 09 '18 at 01:46
  • 2
    You can also look at J.-P. Allouche, H. Cohen, Dirichlet series and curious infinite products, Bull. Lond. Math. Soc. 17 (1985), 531–538. best wishes jpa – jean-paul allouche Aug 07 '20 at 09:40
  • @JyrkiLahtonen It is still an open problem to determine whether those are all the zeros. – Klangen Nov 15 '20 at 10:31

1 Answers1

5

I claim that, for non-integers $z$ with $\Re z > 0$, the following holds: $$ \mathcal{L}(z) = \frac{1}{\Gamma(-z)} \int_0^\infty t^{-z-1} \prod_{k=0}^\infty (1-e^{-2^k t})\,dt.$$ Here's my way to get it. Let $a_1, \ldots, a_n, b$ be positive real numbers, and $z$ be a non-integer complex number with $\Re z < n$. Then $$ \int_0^\infty t^{-z-1} e^{-bt} \prod_{k=1}^{n} (1-e^{-a_k t})\,dt = \Gamma(-z) \sum_{c\in\{0,1\}^n}(-1)^{c_1+\ldots+c_n}(b+c_1 a_1+\ldots+c_n a_n)^z.$$ This may be proven by induction on $n$ (here's the reason of introducing $b$). Now take $a_k=2^{k-1}$: $$ \int_0^\infty t^{-z-1} e^{-bt} \prod_{k=0}^{n-1} (1-e^{-2^k t})\,dt = \Gamma(-z) \sum_{k=0}^{2^n-1} t_k (b+k)^z$$ (where $t_k$ is the sequence in the question), and it remains to take $n\to\infty$ and $b \to 0$.

metamorphy
  • 43,591