7

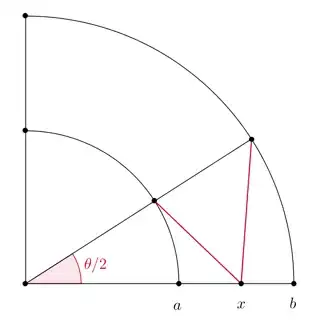
I have the following function of $x$ $$f(x)=\max \left\{\sqrt{a^2+x^2-2ax\cos\left(\frac{\theta}{2}\right)},\sqrt{b^2+x^2-2bx\cos\left(\frac{\theta}{2}\right)}\right\}$$ where $x>a$ and $b>x$. $\theta$ can be any value from $0$ to $\pi$. $a,b,\theta$ are constants and I want to minimize this function with respect to $x$. I know that the derivative of the first term is positive but still I can not find how to solve this problem because of dependence on $\theta$.

Any help in this regard will be much appreciated. Thanks in advance.

I am extremely thankful to @Jack D'Aurizio and @Yves Daoust for their answers. Specially the image that was added by @Jack D'Aurizio which helped me understanding the above problem. Although we can follow the steps mentioned by these two people to find the answer. However, I also have a reasoning (based on the image attached by @Jack D'Aurizio) which also lead to the same answer (I think so). We have to find the optimal value of $x$ in [a,b]. First, we note that as we move from point $a$ toward point $b$ we note that until a certain point ($L$) the first argument increases while the second argument decreases. Therefore, if we are asked to find the optimal point between the interval $[a,L]$ then our answer will be obtained by equating the two arguments of $\max$ function in my first equation (which will be $\frac{a+b}{2\cos(\theta)}$). Now if $\frac{a+b}{2\cos(\theta)} \geq b\cos(\theta)$ then the value of $x$ which minimizes $f(x)$ is actually $b\cos(\theta)$ since if we move further right then both of the arguments of $\max$ function increase. Therefore, moving further right can not be an optimal solution.

Frank Moses
  • 2,778

2 Answers2

16

$$f(x)=\max\left(\|x-ae^{i\theta/2}\|,\|x-be^{i\theta/2}\|\right) $$ hence by assuming $a>0$ we are in the following configuration:

enter image description here

Now consider that

  1. The distance from a point is a convex function;
  2. If $f,g$ are convex functions, $\max(f,g)$ is a convex function;
  3. Convex functions over convex domains attain their maxima at the boundary;
  4. The locus of points $P$ such that $\max(PA,PB)=d$, if non-empty, is given by the union of two circle arcs, symmetric with respect to the perpendicular bisector of $AB$;
  5. Let $A=ae^{i\theta/2}$ and $B=be^{i\theta/2}$. The previous points ensure that the solution of the minimization problem is given by the the projection of $B$ on the $ab$ line, if this point belongs to the $ab$ segment. Otherwise the solution is given by one of the endpoints of $ab$. This is the only part in which $\theta$ plays an active role.

I will let you finish.

Jack D'Aurizio
  • 361,689
  • I want to find $\min f(x)$ with respect to $x$. Please add some steps. Thank you – Frank Moses Apr 04 '18 at 08:35
  • I think your answer find the value of $f(x)$. Right? – Frank Moses Apr 04 '18 at 08:39
  • 3
    @FrankMoses: I added some steps and a geometric description of the solution. The computations should be straightforward now. – Jack D'Aurizio Apr 04 '18 at 08:45
  • As you have commented on another answer (which is removed now), does your answer helps in finding $\min f(x)$ or helps in finding $f(x)$? – Frank Moses Apr 04 '18 at 08:57
  • 3
    @FrankMoses: you can clearly see what is $f(x)$ and the answer describes $\min_x f(x)$ in a explicit way. – Jack D'Aurizio Apr 04 '18 at 09:01
  • Many many thanks Jack. Your figure illustration was really helpful in understanding the problem. I have also written my reasoning in my question to find the answer. Please check if it is right. Thank you again. – Frank Moses Apr 05 '18 at 01:23
6

Hint:

The two arguments are equal when

$$x^2-2ax\cos\phi+a^2=x^2-2bx\cos\phi+b^2$$ or

$$\hat x=\frac{a+b}{2\cos\phi}$$ where $0<\cos\phi<1$. With $b>a$, $\hat x>a$ and $\hat x$ reaches $b$ when $\cos\phi=\dfrac{a+b}{2b}$.

So two cases:

  • if $\cos\phi\le\dfrac{a+b}{2b}$, you minimize the second argument over $[a,b]$,

  • if $\cos\phi>\dfrac{a+b}{2b}$, you minimize the second argument over $[a,\hat x]$, and the first argument over $[\hat x,b]$.

The local minima of these expressions are achieved when $\bar x=a\cos\phi$ (resp. $\bar x=b\cos\phi$). The first $\bar x$ is always out of range, and the second also if $b\cos\phi<a$.

Finally, you have to compute the values at the relevant interval endpoints and the local maxima, depending on the existence of $\hat x$ and $\bar x$.