Conventions:
I'll think of braids as running from an "input" side at the top to an "output" side at the bottom.
The strands in $B_n$ can be numbered $1,\dots,n$ on either the input side (top) or output side (bottom).
If $\gamma \in B_n$, then I'll write $\gamma(k)$ for the action of $\gamma$ on the numbering, i.e. if you take the $k$th strand on the input side, and trace it through, it winds up as the $\gamma(k)$th strand on the output side.
I'll write multiplication as follows: $\gamma \delta$ means $\gamma$ first, then $\delta$, i.e. $\gamma$ on top of $\delta$.
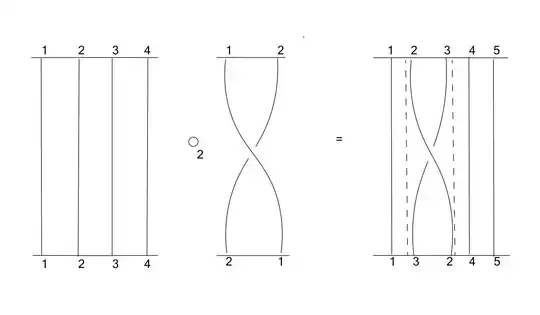
Unless I misunderstand the operation, we have
$$\alpha \circ_k \beta = (i_k \alpha) (D_k^n \beta) = (D_k^n \beta) (i_{\beta(k)} \alpha)$$
where
$i_j : Br_n \to Br_{n+m-1}$ is the inclusion at the $j$th strand: $i_j \gamma$ is a copy of $\gamma$ with $j-1$ identity strands to the left and $n+m-j$ identity strands to the right,
$D_k^n$ is the $n$-fold iterate of the "doubling the $k$th input strand" operator.
So it suffices to understand $D_k$. We have $D_k(\gamma \delta) = D_k(\gamma) D_{\gamma(k)} (\delta)$, so it will suffice to describe $D_k$ on generators. So let $g_j$ be the positive crossing of the $j$th input strand over the $(j+1)$st input strand. Then
$D_k g_j =
\begin{cases}
g_{j+1} & k < j \\
g_{j+1}g_j & k=j \\
g_j g_{j+1} & k=j+1 \\
g_j & k > j+1
\end{cases}$
The same formulas also work if we set $g_j$ to be the negative crossing at the $j$th strand.
I'm not sure if something nice comes out when you put this all together...