2

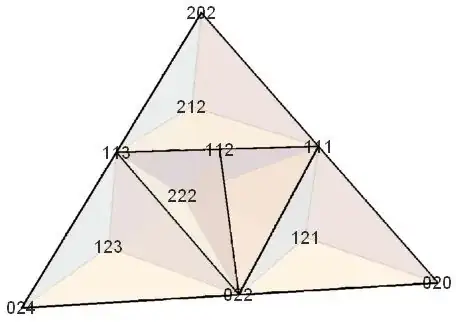
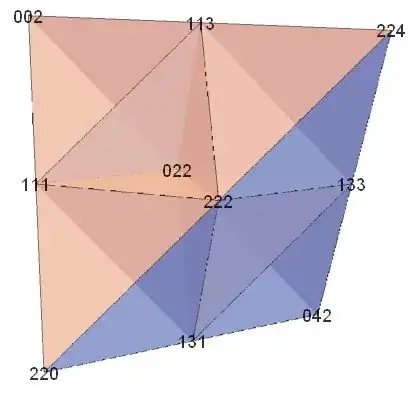
There are a few ways to dissect a non-regular tetrahedron into congruent copies of itself, usually based on orthoschemes. Since there are only five known classes of space-filling tetrahedra, the options are limited. Here are two sample dissections, the first {{020,111,121,022}, {022,111,112,222}, {022,111,121,222}, {022,113,112,222}, {022,113,123,024}, {022,113,123,222}, {111,202,212,113}, {111,222,212,113}} and the second {{002,022,111,113}, {022,042,131,133}, {022,222,111,113}, {022,222,111,131}, {022,222,113,133}, {022,222,131,133}, {111,131,220,222}, {113,133,222,224}}.

self-dissecting tetrahedron 1

self-dissecting tetrahedron 2

Relax the congruency condition and demand only similarity. What are solutions for a non-regular tetrahedron being divided into smaller similar tetrahedra?

Ed Pegg
  • 21,868
  • 1
    Have you considered affine maps of the same subdivisions? – Jap88 Mar 30 '18 at 00:48
  • 1
    When you say "Drop the congruency condition", what restrictions are you requiring on the component tetrahedra? If none, doesn't that just open things up beyond the sense of being answerable? Eg, one infinite family of solutions would be to place one point anywhere in the interior of the tetrahedron, and construct four new tetrahedron using each original face as a base and the new point as the apex. W/out some additional constraints/guidelines, it seems like the answer to "How can you divide a tetrahedron into smaller tetrahedra?" seems to be "Anyway you want." So... Clarification? – WRSomsky Mar 30 '18 at 17:32
  • All component tetrahedra must be similar. An one more condition -- you can only use a finite number of tetrahedra in the dissection. (Cleared up the text) – Ed Pegg Mar 30 '18 at 17:42
  • I'm assuming similar to the original as well as each other? (Asking because in the"congruent" form, they can't be congruent to the original.) And does "similar" include the mirrored forms, or just the ones w/ the same chirality? – WRSomsky Mar 30 '18 at 18:22
  • Yes, similar to the original. And yes, chiral forms are allowed. – Ed Pegg Mar 30 '18 at 18:44

0 Answers0