Why can't $y=xe^x$ be solved for $x$?

Question

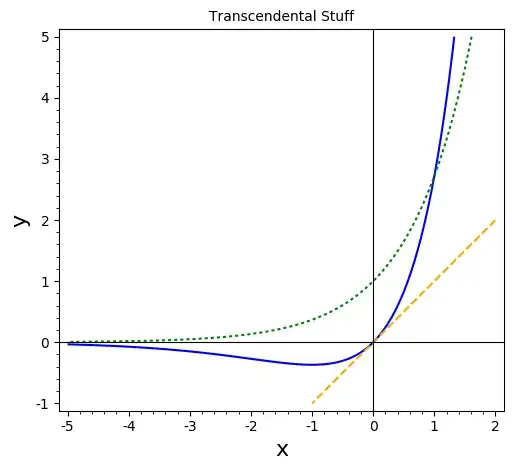
I apologize for my mathematical ignorance regarding this, but could someone help me understand why it isn't possible to (symbolically) find an inverse function for $f(x)=xe^x$?

The most obvious (but presumably the most trivial) is that $f$ does not pass the "horizontal line test". However, if we restrict the domain to $x\geq-1$ this should not be a problem (derivative is positive for $x>-1$ so function is strictly increasing). So now my question becomes: "Why can't we find an inverse function for $f$ over the interval $[-1,\infty)$?"

Perhaps it is because $e^x$ is transcendental (not algebraic). However, we can find an inverse for $g(x) = e^x$, which is also transcendental. Is that because we're "cheating" by defining another transcendental function, namely $\ln(x)$, to be its inverse? In other words, would it be fundamentally no different to define a new function, call it $\text{lnx}(x)$ (if that's not already something else), to be the inverse of $xe^x$ over $[-1,\infty)$ and then say that $f$ has a "closed form" / "symbolic" / ??? inverse function $f^{-1}(x)=\text{lnx}(x)$ over the interval $[-1, \infty)$?

SageMath source to generate plot

xs = (x,-5,2) ys = (y,-1,5) p1 = implicit_plot(x*exp(x)-y,xs,ys, color='blue', legend_label='y=x*e^x') p2 = implicit_plot(x-y,xs,ys, color='orange', linestyle='dashed', legend_label='y=x') p3 = implicit_plot(exp(x)-y,xs,ys, color='green', linestyle='dotted', legend_label='y=e^x') combined = p1 + p2 + p3 combined.axes_labels(['x', 'y']) combined.legend(True) combined.show(title='Transcendental Stuff', frame=True, axes=True, legend_loc='lower right')

See also

• How to know if I can't solve an equation with "standard" methods? (this had some helpful answers & comments)
• If this equation can't be solved algebraically, can it be solved some other way?
• Is there a theory of transcendental functions?
• Is there a proof that there is no general method to solve transcendental equations?

Answer 1

You can use the Lambert-$W$ function to solve it symbolically.

$y = xe^x$ gives $x = W(y)$.

You may run solve(x*exp(x)-y,x) on SymPy Live as an alternative to SageMath.

Answer 2

It can be solved by inventing new functions, but it cannot be solved in closed form using trigonometric, logarithmic or exponential etc. Read this: Chow, Timothy Y. (May 1999), "What is a Closed-Form Number?"

Answer 3

As indicated in the comments and in another answer, there is a special function that has been defined which can serve as an inverse here. However, this doesn't address your basic question, which is: why is this necessary?

Before I talk about that, let me say something about $\ln x$ and $e^x$. Those are both transcendental functions, and they're inverses of each other, but neither is really defined simply to be the inverse of the other. Both of these functions arise very naturally, each on their own. The natural log function is the integral of $x^{-1}$, for a suitably defined integral, and the exponential function is the solution of a differential equation modeling the simplest kind of constant relative growth. They end up being inverses of each other, and that's a cool set of facts to understand and wonder at.

Anyway, you can't use elementary functions to invert lots of things, such as $f(x)=xe^x$. This often happens when we mix different types of functions together. The functions $g(x)=x$ and $h(x)=e^x$ are perfectly invertible, and they are, respectively, polynomial and exponential. The function $f=gh$, on the other hand, is the product of a polynomial function with an exponential function. We expect that to be more complicated. It's not solvable, with the usual algebraic methods, because whatever technique we apply to simplify $e^x$ messes up the polynomial part. Similarly, if you try to solve $e^x(x^2-x)=k$, anything you do to simplify the polynomial part will just make an exponential mess.

It's the blending of different types of functions, which are amenable to transforming with completely different tools, that makes such functions complicated. Other notorious examples include $\frac{\sin x}{x}$, and $e^{x^2}$. It's not always that they're hard to invert, but try doing integral calculus with such functions!

Answer 4

I am going to break your question into two separate questions:

1. Does an inverse function to $y=x \cdot e^x$ exist on the domain $[-1,+\infty)$?
2. Can we find that inverse function in the "standard list" of functions that everyone knows?

Question 1 has an easy answer: yes, that inverse function exists. Its existence is an application of the inverse function theorem which most students first encounter without proof in an ordinary calculus class, and which they then encounter with proof in some kind of advanced calculus class. And then if you're quick enough, you might even be able to attach a name to that function, although it appears that Lambert beat you to it as shown in the answer of @GNUSupporter.

Question 2 is more difficult to answer. First there is no "standard list" of functions that everyone knows. Nonetheless, perhaps that's just because we haven't tried hard enough to list all functions. Can we keep adding functions to the "standard list" until we don't have to add any more? For example, as suggested in the answer of @GNUSupporter, can we just add the "Lambert-W function" $x=W(y)$ to our list if we had never heard of it before, and then declare ourselves happy? Well, maybe, but then you would be perfectly justified to ask whether there is an inverse function to $z=yW(y)$ on some appropriately chosen domain......................

These kinds of questions are addressed (but not definitively answered) in a branch of mathematics called differential algebra which is a kind of broad generalization of differential equations.

Answer 5

$f\colon [-1,\infty)\to\mathbb{R}\colon x\mapsto f(x)=xe^x$ is bijective and has an inverse therefore. The relation Lambert W consists of the branches of the inverse relation of the function $\mathbb{C}\to\mathbb{C}\colon z\mapsto ze^z$.

$f$ is an elementary function (see differential algebra), but Lambert W not.

There are some proofs proving that Lambert W is not an elementary function. See e.g. the following references.

Liouville, J.: Mémoire sur la classification des transcendantes et sur l'impossibilité d'exprimer les racines de certaines équations en fonction finie explicite des coefficients. Journal de mathématiques pures et appliquées 2 (1837) 56–105, 3 (1838) 5233–547

The theorem in Ritt, J. F.: Elementary functions and their inverses. Trans. Amer. Math. Soc. 27 (1925) (1) 68-90 is also proved in Risch, R. H.: Algebraic Properties of the Elementary Functions of Analysis. Amer. J. Math 101 (1979) (4) 743-759.

Ritt, J. F.: Integration in finite terms. Liouville's theory of elementary methods. Columbia University Press, New York, 1948

Rosenlicht, M.: On the explicit solvability of certain transcendental equations. Publications mathématiques de l'IHÉS 36 (1969) 15-22

Bronstein, M.; Corless, R. M.; Davenport, J. H.; Jeffrey, D. J.: Algebraic properties of the Lambert W function from a result of Rosenlicht and of Liouville. Integral Transforms and Special Functions 19 (2008) (10) 709-712