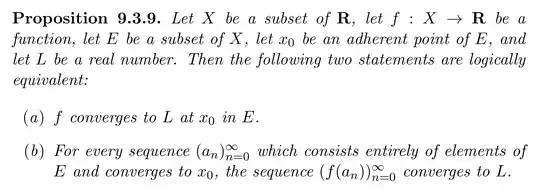2

enter image description here

I'm self-studying from Tao's Analysis. I've got a few ideas about this problem, but I find my "answer" pretty unclear and unconvincing.

There are a number of similar problems in following sections, so I infer that this is a pretty important thing to understand. I'm hoping someone could show a model proof outline so I could understand the structure and fill in the gaps myself.

Here's what I have:

$(a)$ means that for all $\epsilon > 0, \exists \delta >0 $ such that $\forall x \in E$ within $\delta$ of $x_0$, $f(x)$ is within $\epsilon$ of $L$.

To show $(a) \implies (b)$:

In $(b)$, we can interpret the sequence $(a_n)_{n=0}^\infty $ converging to $x_0$ as a sequence of $(x_0+\delta)$ values so that $\delta$s converge to $0$ and $x+\delta$ converges to $x_0$. It's clear that the values $f(x+\delta)$ should converge to $L$.

To show $(b) \implies (a)$:

The sequence $(f(a_n))_{n=0}^\infty$ converges to L, so for each $\epsilon$ there is an $N_\epsilon$ beyond which all $f(a_n)$ are within $\epsilon$ of $L$. Interpret the sequence of $a_n$s as the $x_0 + \delta$ as before.

Hatshepsut
  • 1,364

1 Answers1

4
  • (a) $(\implies)$ (b)

Suppose $f$ converges to $L$ at $x_0$ in $E$, let $(a_n)$ be a sequence of points in $E$ such that $a_n\to x_0$, and let $\epsilon > 0$ be given. Since $f$ converges to $L$ at $x_0$ in $E$, there is some $\delta > 0$ such that if $x$ is in $E$ and $0<|x-x_0| < \delta$, then $|f(x) - f(x_0)| < \epsilon$. Since $a_n\to x_0$, there is some $N\in\Bbb N$ such that if $n > N$, then $0<|a_n - x_0| < \delta$. Thus, if $n > N$, $|f(a_n) - f(x_0)| < \epsilon$.

  • (a) $(\impliedby)$ (b) [Hint.]

Suppose for the sake of contradiction that there were an $\epsilon > 0$ such that for each $n\in\Bbb N$, there was a point $a_n\in E$ such that $0 < |a_n - x_0| < 1/n$, but $|f(a_n)-L| \ge \epsilon$. Produce a contradiction.

Alex Ortiz
  • 26,211