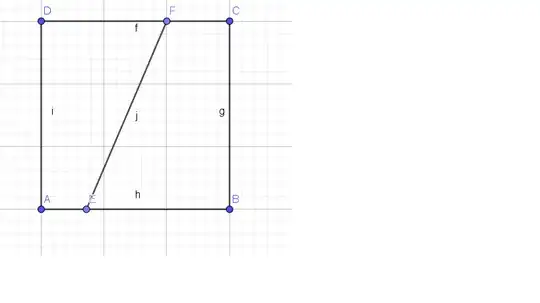
We suppose the points to be uniformly distributed on the respective sides.
You can choose two couples of sides.
For one couple, denotes by $t$ and $s$ the position of the point on the segment, e.g. $A=(0,t),\;B=(0,s)$,
then you shall have
$$
\left\{ \matrix{
0 \le t,s \le 1 \hfill \cr
0 \le \sqrt {1 + \left( {s - t} \right)^2 } \le 6/5 \hfill \cr} \right.\quad
$$
Now
$$
\eqalign{
& 0 \le \sqrt {1 + \left( {s - t} \right)^2 } \le 6/5\quad \Rightarrow \quad 0 \le 1 + \left( {s - t} \right)^2 \le 36/25\quad \Rightarrow \cr
& \Rightarrow \quad 0 \le \left( {s - t} \right)^2 \le 11/25\quad \Rightarrow \quad - \sqrt {11} /5 \le \left( {s - t} \right) \le \sqrt {11} /5 \cr}
$$
And so
$$
\left\{ \matrix{
0 \le t,s \le 1 \hfill \cr
- \sqrt {11} /5 \le \left( {s - t} \right) \le \sqrt {11} /5 \hfill \cr} \right.
$$
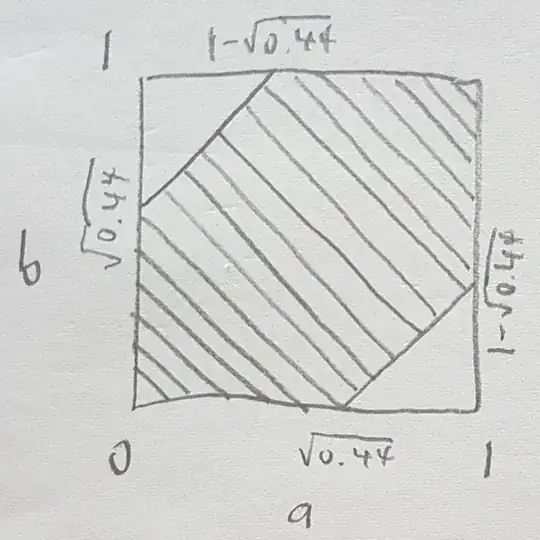
is the portion of the square $1 \times 1$ (on the plane $s,t$) which lies within a stripe of height $\pm \sqrt {11} /5$ from the diagonal.
That is the same scheme as for the "meeting problem".
Take the area of the two excluded triangles $2\left( {1 - \sqrt {11} /5} \right)^{\,2} /2 = \left( {36 - 10\sqrt {11} } \right)/25$
and deduct from that of the unit square to get
$$
\left( {10\sqrt {11} - 11} \right)/25 \approx 0.8866
$$