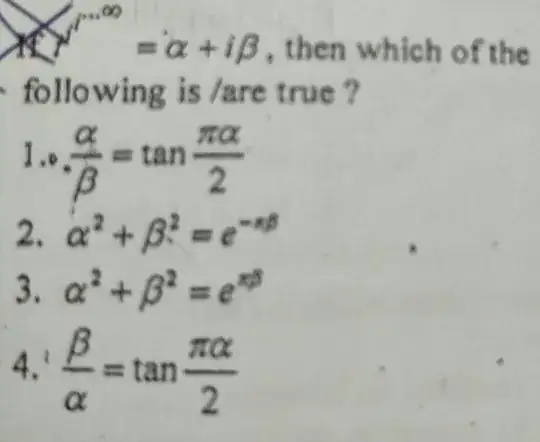If i can find the the value of the expression in lhs. Then i can find the correct option. But i am unable to find the value of expression on lhs which is i^i^i^i^... Upto infinity . How to find that. I tried to convert this to equation i^m=m but i cant proceed further.
Every level of exponentiation is multi-valued. Suppose we always pick the branch $i=e^{i\pi/2}$ in every level. Then we have
$$(e^{i\pi/2})^{\alpha+i\beta}=e^{-\pi\beta/2}\left(\cos\frac{\pi\alpha}{2}+i\sin\frac{\pi\alpha}{2}\right)=\alpha+i\beta.$$
Two simultaneous equations for real $\,\alpha\,$ and $\,\beta\,$ are established by comparing the real and imaginary parts. We have
$$\left\{\begin{array}{l} e^{-\pi\beta/2}\cos\displaystyle\frac{\pi\alpha}{2}=\alpha,\\ \ \\ e^{-\pi\beta/2}\sin\displaystyle\frac{\pi\alpha}{2}=\beta.\\ \end{array}\right.$$
Therefore $\,\alpha^2+\beta^2=e^{-\pi\beta}\,$ and $\,\frac{\beta}{\alpha}=\tan\frac{\pi\alpha}{2}$ can be found without numerically solving for $\,\alpha\,$ and $\,\beta$. Their numerical values are given by $\,\alpha=0.4383\,$ and $\,\beta=0.3606$.
Let $i^{i^{i^{\cdots}}}=\alpha+i\beta$ so $i^{\alpha+i\beta}=\alpha+i\beta$, now take logs of this \begin{eqnarray*} (\alpha+i\beta)i \frac{\pi}{2} =\ln(\alpha^2+\beta^2)+i \tan^{-1}( \beta / \alpha). \end{eqnarray*} Consider the imaginary parts ....
