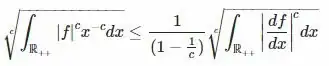I need to prove the following inequality:
for a given $c\in\mathbb R _{>1}$ and for all $f\in W^{1,c}_0(\mathbb R_{++})$.
How can I prove that? I tried to to take $f_n\in C^\infty(\mathbb R_{++})$ compactly supported such that $f_n\rightarrow |f|,$ but it got me nowhere. These techniques always get me confused since there are so many theorems involved.
(Note: the proof of this is given here, though all answers use different techniques then the one above).
We want the inequality to hold for all $f\in W^{1,p}_0(0,\infty)$, however we'll follow a different path than the one you outlined. I'll leave some details to you.
First it's enough to prove that the inequality holds for $f\in W^{1,p}_0(0,\infty)$ with $f\geq 0$: Simply decompose a general $f=\max\{ f,0\} - \max\{ -f,0\}$ and note that these last two functions (and their derivatives) have disjoint supports (up to measure zero sets and so on).
Second we claim that any $f\in W^{1,p}_0(0,\infty)$ with $f\geq 0$ can be approximated by non-negative functions in $C_c^\infty(0,\infty)$: Fix such an $f$, then by definition there exists $g_n\in C_c^\infty(0,\infty)$ converging to $f$ in $W^{1,p}_0(0,\infty)$. Now if $g_n\geq 0$ we're done otherwise $|g_n|\in W^{1,p}_0(0,\infty)$ and has compact support so we can use the standard mollification argument to produce $h_n\in C_c^\infty(0,\infty)$, $h_n\geq 0$ and $h_n$ close to $g_n$. The sequence $h_n$ does the trick.
Finally to pass to the limit in the inequality first fix $f\in W^{1,p}_0(0,\infty)$ with $f\geq 0$ and notice that we may assume (take a subsequence of your approximating sequence if necessary) that $h_n\to f$ a.e. in $(0,\infty)$, but then by Fatou's Lemma \begin{equation} \begin{split} \int_0^\infty f^p x^{-p}\, dx &\leq \liminf \int_0^\infty h_n^p x^{-p}\, dx \\ &\leq \liminf \left(\dfrac{p}{p-1}\right)^p \int_0^\infty |h_n'|^p\, dx \\ &= \left(\dfrac{p}{p-1}\right)^p \int_0^\infty |f'|^p\, dx. \end{split} \end{equation}
