8

There are a few nice discussions about ROA covering a few subtopics:

  1. Region of attraction of : $x'=-y-x^3,y'=x-y^3$ via Lyapunov Function
  2. Region of attraction and stability via liapunov's function (No2)
  3. Basin of attractions with continuity and discontinuity
  4. Strength of attraction of fixed points
  5. Can the basin of attraction be multiple intervals?

Now, consider the following simplest example:

$$\dot{x} = x(x-1)(x+1)$$ $[-1,1]$ is the ROA.

Now consider the two dimensional case:

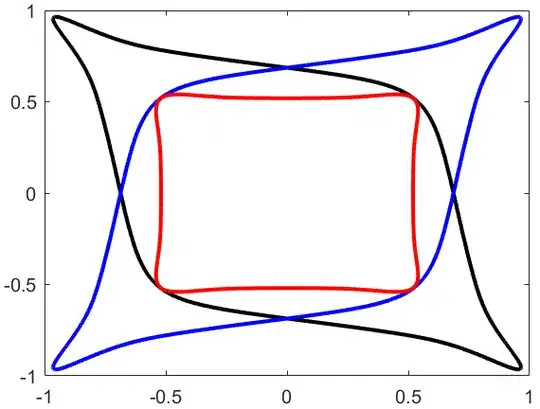
\begin{equation} \begin{aligned} &\dot{x} = x(x-1)(x+1)\\ &\dot{y} = y(y-1)(y+1) \end{aligned} \end{equation}Obviously, ROA is a square. However, if I consider the following coupled ODE:

\begin{equation} \begin{aligned} &\dot{x} = x(x-1)(x+1) + \epsilon (y-x)\\ &\dot{y} = y(y-1)(y+1) + \epsilon (x-y) \end{aligned} \end{equation} where $\epsilon$ is a very small number. Or

\begin{equation} \begin{aligned} &\dot{x} = x(x-1)(x+1) + \epsilon (-y+x)\\ &\dot{y} = y(y-1)(y+1) + \epsilon (-x+y) \end{aligned} \end{equation} Then I have the following ROAs: (blue line-case three, black line-case two, red line-case one)

enter image description here

My questions are:

  1. There are two different tilt directions for case two and three. I know this is because of the slope of the coupling term (for case two, the slope of $x$ and $y$ in the coupling terms are $-1$). But how could I analyze this formally?

  2. Is it a good way to analyze 1. by perturbation method (I think this should be a regular perturbation method)? (observe the sign of the leading order term of the solution obtained from perturbation method?) and how could I proceed it for the coupling term?

Note: It is simple to check that if you just use the linearization method to find the Jacobian matrix (w.r.t the point $(0,0)$), the ROA will be the whole $\mathbb{R}^2$, which is not correct.

Rodrigo de Azevedo
  • 23,223
sleeve chen
  • 8,576
  • 2
    I think geometry and few basic facts for dynamical systems on the plane would be enough here. When you are speaking about basins of attraction for planar systems a boundary of such basins usually consists of unstable limit cycles or union of stable separatrices of saddles with equilibria. When $\epsilon = 0$ the boundary of attraction region consists of saddle equilibria at $(1, 0)$, $(0, 1)$, $(-1, 0)$, $(0, -1)$, their stable separatrices and unstable nodes at $(1, 1)$, $(-1, 1)$, $(-1, -1)$, $(1, -1)$. If you are interested in small values of $\epsilon$, all you have to do is to check ... – Evgeny Feb 11 '18 at 07:19
  • 2
    ... how saddles move when $\epsilon$ changes and in what direction their stable eigenspace rotates. This would give you an explanation why ROA is tilted in one way or another. (Also, I disagree with the red curve as a boundary of ROA) – Evgeny Feb 11 '18 at 07:22
  • @Evgeny The red curve is the one approximated by some numerical methods; therefore it is not a perfect square. – sleeve chen Feb 11 '18 at 07:26
  • Interesting question. How did you obtain the three curves? I‘am only familiar with approximation via Lyapunov functions, however this way is mostly rather conservative... – Carlos Feb 11 '18 at 08:15

0 Answers0