0

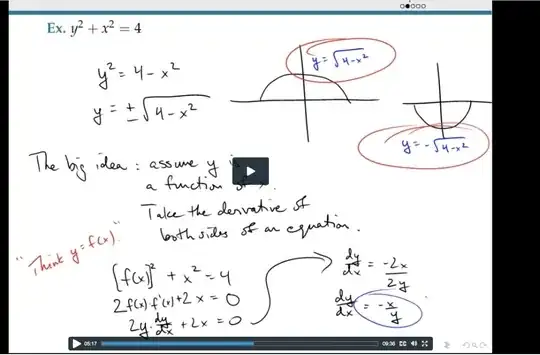
I've encountered this example of implicit differentiation. The problem asks us to find the derivative of $y^2 + x^2 = 4$

enter image description here

How can they assume that y is a function x when it clearly is not? If we isolate y, we get: $y = \pm \sqrt{4-x^2}$. So then how can we assumt that y is a function of x?

On a high level, I'm still a bit confused. So I guess implicit differentiation is useful when we have relations between y and x that aren't functions. That's why the $\frac{dy}{dx}$ is in term of 2 variables. $\frac{dy}{dx}$ has two values depending on the value of x and the value of y since at x, there are 2 values of y. Is that right?

Jwan622
  • 5,908

2 Answers2

1

First, let's double-check the answer they found:

$$ y^2+x^2=4 \rightarrow y=\pm\sqrt{4-x^2} $$ Case 1: $y=\sqrt{4-x^2}$

$$ \frac{dy}{dx}=\frac{1}{2}(4-x^2)^{-0.5}(-2x)=-\frac{x}{\sqrt{4-x^2}}=-\frac{x}{y} $$

Case 2: $y=-\sqrt{4-x^2}$

$$ \frac{dy}{dx}=-\frac{1}{2}(4-x^2)^{-0.5}(-2x)=\frac{x}{\sqrt{4-x^2}}=\frac{x}{-(-\sqrt{4-x^2})}=-\frac{x}{y} $$

Now to your confusion. When you said $y$ is not a function of $x$ because $y=\pm\sqrt{4-x^2}$, you were contradicting yourself because clearly, $y$ is a function of $x$, namely $y=f(x)=\sqrt{4-x^2}$ or $y=f(x)=-\sqrt{4-x^2}$. Which one is the function depends on the conditions on $y$. For example, if the problem says that $y$ is always positive, we will know that $y=\sqrt{4-x^2}$. $$$$The ambiguity in the actual form of $y$, however, does not affect the relation between $\frac{dy}{dx}$ and $x$, as found in the answer by using implicit differentiation. $$$$ Note that we must know whether $y$ is a function of $x$ or $x$ is a function of $y$ when doing implicit differentiation. This is important because $y=f(x)$ does not necessarily mean a function $x=f^{-1}(y)$ exists.

A Slow Learner
  • 1,221
1

Osama Ghani has pointed out the right idea to have in mind. I'll just add a bit of detail to what he is hinting at.

We know the set of solutions to the equation $$y^2+x^2=4$$ is simply the circle of radius 2. You are certainly correct in pointing out that the circle is not the graph of a differentiable function of $x$. However, let's not forget that the operation of differentiation is a local one -- we take the derivative at each point of a given function.

Then the crucial idea is that for each point on the circle $(x,y)\in \{(x,y)\in \mathbb{R}^2:x^2+y^2=4\}$, if we intersect a small ball (centered at $(x,y)$) of some radius $\delta$ with the circle, we do in fact get the graph of a function -- it looks like an arc on the circle. This function depends on the chosen point and its domain is restricted according to the radius $\delta$. The observation you made is simply that these local functions are not the restrictions of a globally defined function.

Note also that the final answer for $\frac{dy}{dx}$ (when solved implicitly) depends on both $x$ and $y$ and not simply $x$. This again is because $y$ is not globally a function of $x$. You need to specify a pair $(x,y)$ to give a locally defined function $y(x)$, whose graph contains the point $(x,y)$.

  • Is this true for all problems related to implicit differentiation? They always involve functions where we need to specify a pair? Also, slightly confused at: each point on the circle (x,y)∈{(x,y)∈ℝ2:x2+y2=4}... the x and y are actually on the circumference of the circle right? – Jwan622 Feb 02 '18 at 15:06
  • tad confused at this part: Then the crucial idea is that for each point on the circle (x,y)∈{(x,y)∈ℝ2:x2+y2=4}(x,y)∈{(x,y)∈R2:x2+y2=4}, if we intersect a small ball (centered at (x,y)(x,y)) of some radius δδ with the circle, we do in fact get the graph of a function -- it looks like an arc on the circle – Jwan622 Feb 02 '18 at 15:06
  • @Jwan622 Well, technically you always need to specify a point at which your taking a derivative. In the case of implicit differentiation, you need to specify a $y$ value so that you know which part of the set you want to view as the graph of the function. In practice however, you can just sort of follow your nose -- take the derivative (assuming $y$ is locally a function of $x$) with respect to $x$ and see what happens –  Feb 02 '18 at 16:53
  • @Jwan622 The answer was supposed to dissolve the confusion about why you can make the assumption that $y$ is a function of $x$. Again, the key is this is true only locally. –  Feb 02 '18 at 16:55