"Flipping" a circulant matrix in the time dimensional sense:
$$\left[\begin{array}{ccc}1&16&4\\4&1&16\\16&4&1\end{array}\right] \to \left[\begin{array}{ccc}4&16&1\\16&1&4\\1&4&16\end{array}\right]$$
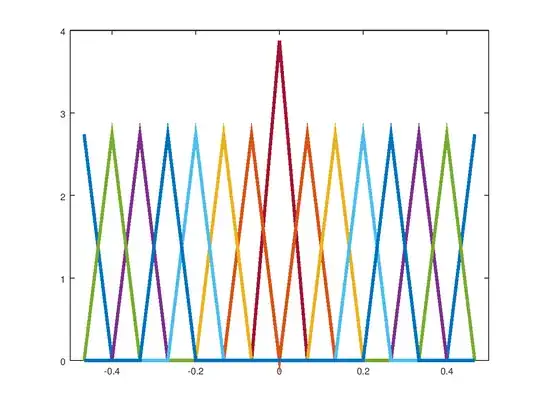
breaks the eigensystem so that it is no longer sure to be the complex exponentials. But indeed if we look at the power spectrum of the rows of $\bf V, M=VDV^T, VV^T=I$ some random such matrix $\bf M$, we do indeed get a very clear symmetry with all power distinctly spread symmetrically around the 0 frequency, seemingly atomic:
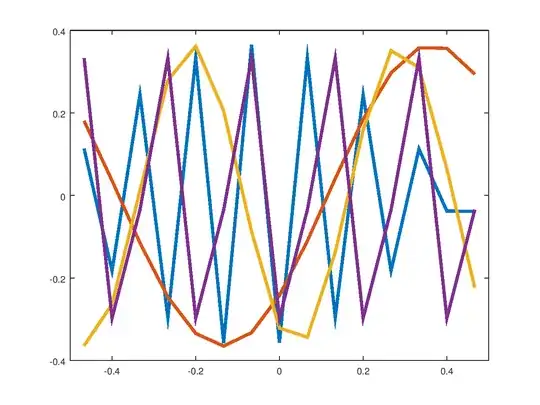
In the time domain the first four rows of $\bf V$ look like this:
And we can see a clear periodic pattern of different frequencies, although not perfect Fourier basis functions.
Peculiarly, all of them also seem to be real valued, and the eigenvalues as well! This makes me suspect they could be related to the Fourier transform basis functions. Something like it's annoyingly suspiciously well behaved twin or something.
Can we derive some expression for those functions?