6

I have considered a sequence defined as follows:

$$a_{n+1}=a_n+\log a_n$$

$$a_1=2$$

Surprisingly enough, its growth is almost linear, or, more precisely, it seems that:

$$n < a_n < n^{3/2}$$

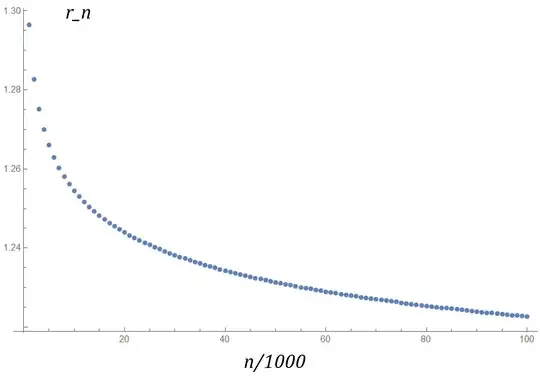
From numerical experiments, the growth rate for large $n$ is well described by a power law (as it's obvious from the previous condition), with the exponent being around $1.2$. Here's the plot of:

$$r_n=\frac{\log a_n}{\log n}$$

for $n=10^3 - 10^5$.

enter image description here

For larger $n$ we have, for example:

$$r_{0.5 \cdot 10^6}=1.204993305$$

$$r_{1.5 \cdot 10^6}=1.194589226$$

$$r_{4.5 \cdot 10^6}=1.185287843$$

$$r_{10 \cdot 10^6}=1.179122734$$

$$r_{20 \cdot 10^6}=1.174129607$$

Can we (1) prove that the sequence obeys a power law for $n \gg 1$ and (2) find the value of $r_{\infty}$?

Edit

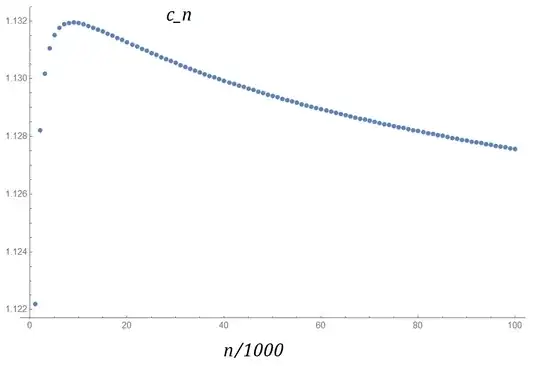
If, as Did says in the comments, the sequence actually obeys another law:

$$a_n \asymp c n \log n$$

Then it would be interesting to prove and especially find $c$.

From experiments:

$$c_{10 \cdot 10^6}=1.113128774$$

$$c_{20 \cdot 10^6}=1.111029684$$

And the plot for $n=10^3 - 10^5$:

enter image description here

Professor Vector suggested that $c_{\infty}=1$, which is possible even though convergence is really slow.

Update:

In a linked question I prove (kind of) that the following inequality holds for $n \geq 2$:

$$a_n \leq (n+1) \left( \ln (n+1) + \ln \ln (n+1) \right)$$

This bound is quite tight.

Yuriy S
  • 32,728
  • Just out of curioisity : did you create the problem ? It is nice. – Claude Leibovici Jan 30 '18 at 10:26
  • @ClaudeLeibovici, thank you. Yes, it's yet another random idea I had. – Yuriy S Jan 30 '18 at 10:27
  • 1
    Naturally, one expects that $$a_n\sim cn\log n$$ – Did Jan 30 '18 at 10:28
  • @Did, I would be grateful if you elaborate on this, if you have the time. In that case finding $c$ would be interesting. I'll conduct some experiments – Yuriy S Jan 30 '18 at 10:32
  • More precisely, I'd expect $a_n\sim n\log n$, i.e. $c=1$. –  Jan 30 '18 at 10:35
  • 1
    Unless I'm mistaken, a careful induction argument should prove that $$n\log n - n \leq a_n \leq n \log n + n$$ for all $n \geq 2$. – Antonio Vargas Jan 30 '18 at 10:53
  • @AntonioVargas My calculations suggest $a_{2321}^{,} > 2321 \log 2321 +2321$ – Henry Jan 30 '18 at 11:07
  • @AntonioVargas The upper bound is certainly wrong, it's more like $n (\log n + \log\log n)$, I think (that's why convergence is so slow). –  Jan 30 '18 at 14:14
  • @ProfessorVector I agree. – Antonio Vargas Jan 30 '18 at 19:16
  • 1
    The nasty physicist way:

    First of all, from your inital condition $a_1=2$ it is obvious that $a_n\rightarrow +\infty$.

    Furthermore, approximate $a_{n+1}-a_n\approx a'_{n}$ (we will justify this in hindsight). This yields ($n\rightarrow x,,a_n\rightarrow y(x)$) $$ y'(x)=\log(x) \rightarrow x=\int\frac{dy}{\log(y)} $$

    which might be implicitly solved in terms of the logarithmic integral $\text {li}(z)$

    $ x=\text {li}(y)+C $

     – tired Feb 25 '18 at 22:26
  • 1
    since we are interested in the limit of $x\rightarrow\infty$ we can neglect the constant $C=\text{li}(2)-1$ and use the approximation $\text{li}(z)\sim z/\log(z)$ (Proof integration by parts). So

    $$ x\sim\frac{y}{\log(y)}+O\left(\frac{1}{\log(y)}\right) $$

    or

    $$ y(x)\sim -x W_{-1}\left(-\frac{1}{x}\right) $$

     – tired Feb 25 '18 at 22:26
  • 1
    where $W_{-1}(z)$ is the ($-1$ branch) of the Lambert-W function. The other branches don't fullfil the correct boundary conditions and can be therefore dismissed. Using known asymptotics, we obtain

    $$ y(x)\sim x\log(x) $$

    as expected.

    Now, $y^{(n)}(x)\sim x^{-n-1}\ll y'(x) = \log(x)+1$ which justifies our inital approxmation (the higher order corrections to the difference between $\Delta a_n$ and $a'_{n}$ negligible). So

    $$ a_n\sim n \log(n)\quad \text{as} ,,n\rightarrow \infty $$

     – tired Feb 25 '18 at 22:26
  • @tired, this is amazing. I hope you would post this as an answer – Yuriy S Feb 25 '18 at 22:31
  • @YuriyS thanks,but i think there are too many technical points here which have to made rigorous to make this a proper answer. but i have no time for that at the moment so this is all for now.. :( – tired Feb 25 '18 at 22:38
  • @tired, of course. But what's important: your method works for a very general kind of sequences and doesn't require guessing. I'm definitely going to use it – Yuriy S Feb 25 '18 at 22:46
  • this is true:as long as $|a'_n-a^{(m)}_n|\ll1$ you should be fine using it :) – tired Feb 25 '18 at 22:48
  • one last thing: a detailled account of the asymptotics of Lambert-W might be found here: https://cs.uwaterloo.ca/research/tr/1993/03/W.pdf – tired Feb 25 '18 at 22:54
  • interesting...the $x \log(\log(x))$ correction comes nearly for free using my method...maybe i write soemthing up on wednesday – tired Feb 26 '18 at 18:35
  • A good approximation of $a_n$ using the inverse logarithmic integral can be found here. I will use this to give an answer to the linked question – Helmut Jun 08 '19 at 10:13
  • @tired Your initial approximation that $n\approx\mbox{ li},(a_n)+C$ is much better than $a_n\sim\log(n)/n$ as is shown here – Helmut Jun 17 '19 at 15:04

2 Answers2

3

It isn't a power law, and $\lim_{n\to\infty}r_n=1$. One way to prove this is to check by induction that $a_n\leq 2n\log n$ for every $n\geq 2$.

Especially Lime
  • 46,692
3

Hint. Note that if we show that eventually $$c_1 n\ln n\leq a_n \leq c_2 n\ln n\quad \text{with $0<c_1\leq c_2$}$$ ($c_1=1/2$ and $c_2=2$ should work by induction), then $\ln(a_n)\sim \ln(n)$, and, by Stolz-Cesaro Theorem, $$\lim_{n\to +\infty}\frac{a_n}{n\ln n}=\lim_{n\to +\infty}\frac{a_{n+1}-a_n}{(n+1)\ln (n+1)-n\ln(n)}= \lim_{n\to +\infty}\frac{\ln(a_n)}{\ln ((1+1/n)^n)+\ln(n+1)}=1.$$

Robert Z
  • 147,345