The IVP $\begin{cases}\dot{x}=x^3+e^{-t^2}\\x(0)=1\end{cases}$ possesses a solution in $I=(-1/9,1/9)$

Question

I'm stuck with this problem:

Prove that the IVP

$$\begin{cases}\dot{x}=x^3+e^{-t^2}\\x(0)=1\end{cases}$$

has an unique solution defined on $I=(-1/9,1/9)$. Which is the largest interval of definition of the solution? We can extend that solution to $t=1$?

Okay, so it's obvious that $f(t,x)=x^3+e^{-t^2}$ is locally Lipschitz with respect to $x$, and it's continuous too. So by Picard we can find a unique solution defined on $\mathbb{R}$.

But then the exercise wouldn't have any sense, so I think that I'm doing something wrong.

Thanks for your time.

Answer 1

Fact 1. The flux function $f(t,x)=\mathrm{e}^{-t^2}+x^3$ of our ODE is $C^1$ in $x$, and hence locally Lipschitz, and therefore our IVP enjoys uniqueness.

Fact 2. Since the flux function is smooth in the whole $\mathbb R^2$, then our IVP possesses a solution $\varphi$ defined on a maximal open interval $(a,b)$. If $a$ is finite then $\lim_{t\to a^+}\varphi(t)\in\{-\infty,\infty\}$, and similarly, if $b$ if finite then $\lim_{t\to b^-}\varphi(t)\in\{-\infty,\infty\}$.

Fact 3. The unique and maximally defined solution of $$ x'=g(t,x)=x^3,\,\, x(0)=1, $$
is $\psi(t)=(1-2t)^{-1/2}$, defined in the maximal interval $\big(-\infty,\frac{1}{2}\big)$.

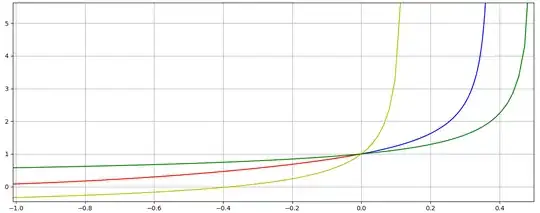
Fact 4. Clearly $\,g(t,x)<f(t,x),\,$ and since $\varphi(0)=\psi(0),\,$ then $$ \varphi(t)>\psi(t), \quad \text{for all t>0}, $$ thus $\varphi$ blows up for some $t\in \big(0,\frac{1}{2}\big]$, and hence $\varphi$ CAN NOT be extended until $t=1$.

Fact 5. Consider now the Picard iterative sequence which converges to $\varphi$: $$ \varphi_0(t)=1, \quad \varphi_{n+1}(t)=1+\int_0^t \big(\varphi_{n}(s)^3+\mathrm{e}^{-s^2}\big)\,ds. $$ We shall show that, $$ |\varphi_n(t)|\le 2, \quad \text{for all $n\in\mathbb N$ and $|t|\le 1/9$.} $$ For $n=0$ is given. Assume that this holds for $n=k$. Then for $n=k+1$ and $|t|\le 1/9$, we have that $$ |\varphi_{k+1}(t)|=\left|\,1+\int_0^t \big(\varphi_{k}(s)^3+\mathrm{e}^{-s^2}\big)\,ds\,\right|\le 1+ \int_0^t\big| \,\varphi_{k}(s)^3+\mathrm{e}^{-s^2}\big|\,ds\le 1+\frac{1}{9}\big(2^3+1\big)=2, $$ and hence $$ \Big[-\frac{1}{9},\frac{1}{9}\Big]\subset (a,b), $$ and hence $\varphi$ is defined for $|t|\le 1/9.$

Fact 6. Let $h(t,x)=x^3+1\ge f(t,x)$. Then the solution $\vartheta$ of $$ x'=h(t,x), \quad x(0)=1, $$ is definable in the whole $(-\infty,0]$, and since $\varphi(t)\ge \vartheta(t)$, for $t\le 0$, and $\varphi$ is increasing, then clearly $\varphi$ is also definable in the whole $(-\infty,0]$.

Answer 2

Local existence and uniqueness

As has already been said, the ODE is smooth and thus existence and uniqueness of local solutions is guaranteed. Assume that $x:(\alpha,\beta)\to\Bbb R$, $α<t_0<β$ is a maximal solution. At this point we know that it exists, but have no quantitative information on $α$ and $β$.

Strategy for proving the claim

Now if it can be proven that some easily accessible continuous functions are bounds of $x$ on some interval $[a,b]$, $l(t)\le x(t)\le u(t)$ for $t\in [a,b]$, then certainly $α<a$ and $b<β$, as the values $x(a)$ and $x(b)$ have to exist at least as limits, and can be taken as initial points whose local solutions extend the solution $x$ over the interval $[a,b]$. Additionally if the lower bound goes at some point to $+\infty$ or the upper bound to $-\infty$, we can be sure that the solution $x$ can not be extended to reach these times.

Positive half axis

In forward time, $t>0$, the right side is positive so that the solution is increasing and stays positive. Then one can find upper and lower bounds for the right side of the ODE, the slope of $x$, $$ x^3< \dot x\le x^3+1<(x+1)^3. $$ These differential inequalities can be solved as \begin{align} &-2>-2x^{-3}\dot x~\text{ and }~ -2(x+1)^{-3}\dot x>-2 \\[.5em] \implies& \frac{d}{dt}(x^{-2})<-2<\frac{d}{dt}((x+1)^{-2}) \\[.5em] \implies& x^{-2}-1<-2(t-0)<(x+1)^{-2}-\frac14 \end{align} This can be resolved to $$ \frac1{\sqrt{1-2t}}<x(t)\text{ and }x(t)<\frac2{\sqrt{1-8t}}-1 $$ which means that the solution remains bounded and thus exists on $[0,\frac18)$ and will go to infinity before $t=\frac12$.

Negative half axis

Similar estimates are possible for negative $t<0$ resulting in $$ \frac2{\sqrt{1-8t}}-1<x(t)<\frac1{\sqrt{1-2t}} $$ which is valid (at least) as long as the assumption $x(t)>0$ is supported by the lower bound, $1-8t<4$ or $t>-\frac38$.

Conclusion

In total we find that the maximal interval includes the interval $[-\frac38,\frac18)$ which includes the claimed interval $(-\frac19, \frac19)$.

Numerical computation and plots

confirm the bounds and that there is a pole in the positive direction red-blue - numerical solution; green, yellow - bounding functions

Appendix A: Alternative bound on the positive half axis

As a second thought, use $1\le x$ for $t>0$ to get $\dot x\le x^3+1\le 2x^3$ as upper bound which after separation integrates to $$x(t)\le \frac1{\sqrt{1-4t}}.$$ Thus the solution is guaranteed to exist on the larger interval $[0,\frac14)$.

This means that the maximal interval contains $[-\frac38,\frac14)$.

Appendix B: Numerical-graphical estimation of the pole location

Close to the point $t=β$ of divergence $x$ and $\dot x$ are so large that the ODE in first approximation is $\dot x=x^3$ with solution $x(t)=\dfrac1{\sqrt{2(C-t)}}$. This means that plotting $y=C(t)=t+\frac12x(t)^{-2}$ close to the pole location $β$ should result in an almost constant which is in the limit equal to the point of divergence and allows to read off better estimates of the location of the pole. At the same time the plot has to end at $t=β$, so that the point of intersection is $(β,β)$. As that is on the diagonal $y=t$, plotting it provides an additional aid for a visual inspection.

blue - $y=t+\frac12x(t)^{-2}$; red - $y=t$

which finds the pole at about $t=0.375106$.

Answer 3

So by Picard we can find a unique solution defined on $\mathbb R$.

$f$ not Lipschitz with respect to $x$, but locally Lipschitz with respect to $x$. Same goes for $g(x,t)=-x^2$ and the IVP $$ \begin{cases} \dot x=g(x,t)\\ x(1)=1 \end{cases} $$ has the solution $x(t)=\frac1t$ on $(0,\infty)$ but on $\mathbb R$.