Perfect Pascal Mysticum Points

Question

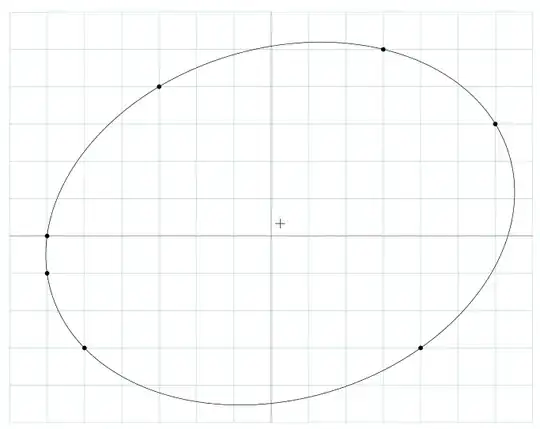
Consider the set of 6 points $((-12,-3), (3,-6), (3,7), (9,-3), (11,-1), (12,1))$. They make an ellipse. No lines generated by the points are parallel. When these points are used to make a Hexagrammum Mysticum, all of the 60 Kirkman Points, 20 Steiner points and 15 Salmon Points are distinct and finite. The 60 Pascal lines, 20 Cayley lines, and 15 Plücker lines are also distinct. As an aside, I learned from Dick Tahta's wonderful Fifteen Schoolgirls that these guys hated each other.

When the initial six points are all rational or in the same root space, the generated points are in the same space. The task at hand is to generate a set of points with at least the first condition, and hopefully more.

1. Generate a set of 6 simple points on a conic section with no parallelism.
2. The 95 Kirkman Steiner Salmon points should be finite and distinct.
3. The 101 points should be human-eye distinguishable in a single image.

I got these 6 points by looking at subsets from 13 point ellipse and Small Lattice Ellipses.

My solution above fails #3. Maybe different root spaces, different approaches or different conic sections will work better.

Answer 1

As far as I know, the following ellipses are the records for smallest (by area) and shortest (by major axis). I specify angles in degrees anticlockwise from horizontal.

The smallest such ellipse is $$10x^2 -9xy + 14y^2 -8x +y-114=0.$$ Its semi-axes are 4.0445 and 2.6151, making its area 33.228. Its centre is $(215/479, 52/479)$. It is inclined at an angle of $33.0188^\circ$. It goes through (4, 2), (3, 3), $(-3, 0)$, $(-3, -2)$, $(-1, -3)$ and $(2, -2)$.

The shortest such ellipse is $$17x^2 -xy +18y^2 -10x -15y -231=0.$$ Its semi-axes are 3.7466 and 3.5982, making its area 42.352. Its centre is $(375/1223, 520/1223)$. It is inclined at an angle of $22.5^\circ$. It goes through (4, 1), (3, 3), (1, 4), $(-3, 2)$, $(-1, -3)$ and $(3, -2)$.

If more examples are wanted, how about an ellipse through $n>6$ integer lattice points, no four of which lie by twos on any two parallel lines.

The smallest and shortest such ellipse through 7 points is $$9x^2-4xy+15y^2-3x-9y-342=0.$$
Its semi-axes are 6.4002 and 4.6941, making its area 94.383. Its centre is $(63/262, 87/262)$. It is inclined at an angle of $16.845^\circ$. It goes through (6, 3), (3, 5), $(-3, 4)$, $(-6, 0)$, $(-6, -1)$, $(-5, -3)$ and $(4, -3)$.

The smallest and shortest such ellipse through 8 points is $$14x^2 -3xy +16y^2 -3x +10y -3086=0.$$ Its semi-axes are 15.2958 and 13.5557, making its area 651.3944. Its centre is $(66/887, -271/887)$. It is inclined at an angle of $28.155^\circ$. It goes through (15, 1), (14, 6), (10, 11), (6, 13), $(-3, 13)$, $(-10, 9)$, $(-14, 3)$, and $(14, -4)$.

The smallest and shortest such ellipse through 9 points is $$18x^2 -13xy +24y^2 -5x +5y -20225=0.$$ Its semi-axes are 38.2265 and 26.8004, making its area 3128.52. Its centre is $(175/1559, -115/1559)$. It is inclined at an angle of $32.6124^\circ$. It goes through (34, 1), (35, 5), (32, 21), (5, 30), $(-3, 28)$, $(-10, 25)$, $(-33, 1)$, $(-27, 26)$ and $(14, -23)$.