9

I recently saw the following puzzle somewhere:

Find a continuous, surjective function $f:\mathbb R\mapsto\mathbb R$ that takes on each of its values exactly three times.

Or, more technically stated,

Find a continuous, surjective function $f:\mathbb R\mapsto\mathbb R$, such that for all $y\in\mathbb R$, there exist exactly three real solutions $x$ to the equation $f(x)=y$.

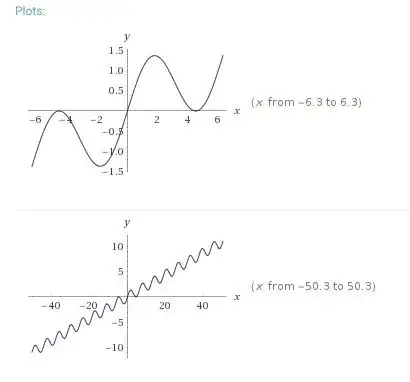
My solution to this puzzle was the function $$f(x)=\sin^2 \frac{3\pi(x-\lfloor x\rfloor)}{2}+\lfloor x\rfloor$$ Since then, I've thought of a few variations on this puzzle, none of which I have been able to solve:

  • Can a function $g:\mathbb R\mapsto \mathbb R^2$ satisfy these requirements? What about a function $h:\mathbb R^2\mapsto \mathbb R$?
  • What function $f$ satisfies the original puzzle, and is also $C^\infty$?
Franklin Pezzuti Dyer
  • 40,930
  • 9
  • 80
  • 174
  • See https://math.stackexchange.com/questions/1030585/can-a-continuous-real-function-take-each-value-exactly-3-times which is itself a duplicate. – Gerry Myerson Dec 28 '17 at 18:28
  • @Nilknarf: It would be a good idea to highlight your actual questions. – celtschk Dec 28 '17 at 19:01
  • There's a smooth example in achille hui's answer to the linked question. – Hans Lundmark Dec 29 '17 at 12:26
  • I didn't say this question is a duplicate. I said that that question was a duplicate, so people would know to trace back to see whether there's anything at either question of interest here. – Gerry Myerson Dec 29 '17 at 14:16
  • Regarding your first question, there is no such $h$, because if $h(x)\neq h(y)$ then by the intermediate value theorem every value between $h(x)$ and $h(y)$ is attained along every path from $x$ to $y$. I.e. every intermediate value is attained infinitely many times. – Yly Dec 29 '17 at 16:21
  • I am convinced that there is no such $g$ either, but it appears considerably more difficult to prove. See this question: https://math.stackexchange.com/questions/43096/is-it-true-that-a-space-filling-curve-cannot-be-injective-everywhere

    They succeed in proving that no injective $g:\mathbb{R}\rightarrow\mathbb{R}^2$ exists, but the proof doesn't seem to extend to the present case.

     – Yly Dec 29 '17 at 16:26
  • @gimusi What about the second question? Did you solve that one? – Franklin Pezzuti Dyer Dec 29 '17 at 22:38
  • @Nilknarf Please, if you are ok, you can accept the answer and set it as solved. Thanks! – user Feb 01 '18 at 22:46

2 Answers2

10

Starting from the following idea:

$$g(x)=\sin x + \frac{2}{3\pi}x$$

g(x) plot

we can adjust the constant for x in such way that

$$f(x)=\sin x + Kx$$

fullfills the given condition.

The value of K can be easily found imposing that:

$$\begin{cases}(\sin x)'=\cos x=-K\\ Kx=-\sin x\end{cases}$$

$$\implies tanx=x \implies x\approx4.49340945790906 \quad K=-\cos x \approx 0.21723362821123...$$

f(x) plot

enter image description here

user
  • 162,563
  • Doesn't work. This function has 4 zeroes. – Franklin Pezzuti Dyer Dec 28 '17 at 18:33
  • @Nilknarf: the idea is correct, however. If $\frac{2}{3\pi}$ is replaced by the solution of a trascendental equation, $\sin(x)+K x$ is an entire function attaining each real value exactly three times. – Jack D'Aurizio Dec 28 '17 at 18:35
  • @Nilknarf why 4 zeros? http://www.wolframalpha.com/input/?i=plot+sinx%2B(2%2F(3pi))x,+x%3D-20..20 – user Dec 28 '17 at 18:37
  • 2
    @gimusi: the correct constant is not $\frac{2}{3\pi}$ but $0.21723362821122\ldots$. The graphs of $\sin(x)$ and $-\frac{2}{3\pi}x$ are not tangent. – Jack D'Aurizio Dec 28 '17 at 18:39
  • @JackD'Aurizio Thanks, it's clear to me now! – user Dec 28 '17 at 18:40
  • @JackD'Aurizio later I'll try to find the equation for this value! – user Dec 28 '17 at 18:43
  • 1
    If I understand it correctly, it should be the $K$ from the simultaneous solution of $\sin x+Kx=0$ and $\cos x+K=0$ on $x$ and $K$ with the smallest possible positive value for $x$. Alternatively, the largest $K$ so that both equations have a simultaneous solution. – celtschk Dec 28 '17 at 19:18
  • 1
    Very nice, gimusi. My apologies if you disliked my edits, I was not sure you would come back and finish this your own way, as you now have. In case of interest: I suspect a similar type of thing, just different $K,$ might give each value exactly five times. – Will Jagy Dec 28 '17 at 21:34
  • @WillJagy I don't dislike but I prefer to complete myself my own answer, you can add another answer with any futher information and graph. Thanks! – user Dec 28 '17 at 21:37
  • I added the graph(s) for five times. – Will Jagy Dec 28 '17 at 22:44
  • 1
    @WillJagy well done! – user Dec 28 '17 at 22:52
2

I like Jack's description, draw a fixed sine curve and find tangent lines through the origin. In this case, I am finding a tangent point with $2 \pi < x < \frac{5 \pi}{2}.$ Under the circumstances, the slope $K$ comes out positive, with $K \approx 0.128374554, $ solution of $$K \left( 2 \pi + \arccos K \right) = \sqrt {1 - K^2}$$ The $x$ value for the tangent is about $7.725251838,$ just below $\frac{5 \pi}{2} \approx 7.853981635$$

enter image description here

This time, we get each value assumed by the function five times, the function being $\sin x - K x.$

enter image description here

Alright, I widened out to include $\pm 14,$ and clicked so it shows the roots and critical points. It says there are critical points at $x \approx \pm 14.008$

enter image description here

Will Jagy
  • 146,052