Lyapunov function and an open disk inside the basin of $(0,0)$

Question

a)Find a strict Lyapunov function for the equilibrium point $(0,0)$ of $$x'=-2x-y^2$$ $$y'=-y-x^2$$. b)Find $\delta>0$ as large as possible so that the open disk of radius $\delta$ and center $(0,0)$ is contained in the basin of $(0,0)$

Solution

a) is done.

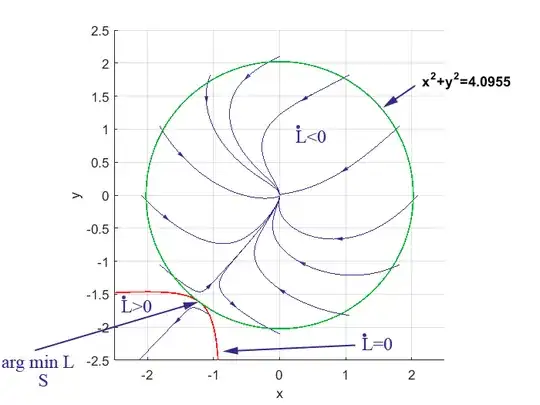
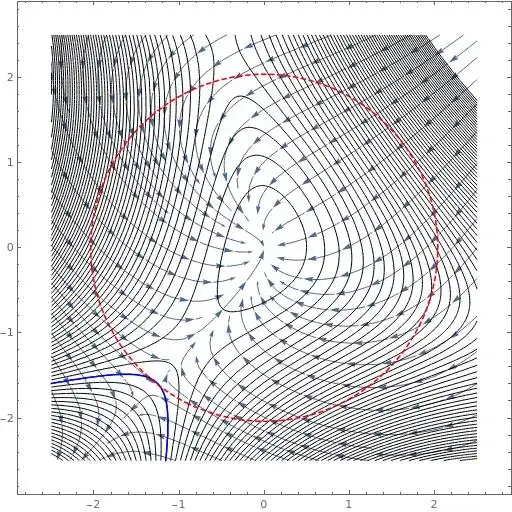
Consider the Lyapunov function $L(x,y)=x^2+y^2$.

$L'(x,y)=-2x^2(2+y)-2y^2(1+x)$ is strictly negative when x and y are near from zero. Switching into polar coordinates: $L'=-2r^3(1+cos^2\theta)[\frac{1}{r}+\frac{cos\theta sin\theta(cos\theta+sin\theta)}{1+cos^2\theta}]$

Now since $\color{blue}{\frac{cos\theta sin\theta(cos\theta+sin\theta)}{1+cos^2\theta}>-\frac{1}{2},}$ as long as $r<2$ the quantity of the brackets is positive.

Thus $L'<0$ is in the open disk of radius 2 with center (0,0).

Moreover, there are $\color{blue}{no}$ solutions on which $L$ is constant except for the equilibrium at $(0, 0). $This implies, by the Lasalle invariance principle, that the circle of radius 2, centered at the origin is contained in the basin of attraction.

---

To say no solutions on which L is constant means that there are no other equilibrium points , i.e the only point is $(0,0)$?

I don't understand the blue part of the solution and also the italic text.

Any kind of help is greatly appreciated.

Answer 1

1. I beleive the simplest way to show that $\frac{\cos\theta\sin\theta(\cos\theta+\sin\theta)}{1+\cos^2\theta}>-\frac12$ is to plot the left part of the inequality: They didn't ask to prove the inequality, right?

2. As one can see, the minimum value of $\frac{\cos\theta\sin\theta(\cos\theta+\sin\theta)}{1+\cos^2\theta}$ is not exactly $-1/2$ (it is approximately $-0.4941$), so it is not quite correct to say that the radius $\delta=2$ is as much as possible.

3. In fact, the LaSalle's Invariance Principle is not needed here. It is intended to use for non strictly negative $\dot L$. Since $\dot L<0$ inside the disk, we can conclude that $L$ is decreasing along the trajectories and replicate the proof of the Lyapunov's theorem on asymptotic stability.

4. The polar coordinates are not needed too. The general way to obtain the largest possible (for a fixed Lyapunov function) subset of the domain of attraction looks as follows.

Suppose we have the Lyapunov function $L(x)$, its derivative is $\dot L(x)$. Consider the set $$ S= \left\{ x: \dot L(x)=0\right\}\setminus \{0\}. $$ Suppose that we can solve the minimization problem $$\tag{1} C=\min_{x\in S} L(x). $$ (For this system, in particular, $C\approx 4.0955$). The level set $$ \Omega_C = \left\{ x: L(x)<C \right\} $$ is the largest possible positive invariant set contained in the domain of attraction of the origin that can be obtained for the fixed Lyapunov functon. This fact can be demonstrated by this picture: The point of intersection of the green and red curves is the minimum point of (1). Indeed, since $L(x)<C$ for any point of the level set $\Omega_C$, this set does not contain points such that $\dot L\ge 0$; at the intersection point the value of $\dot L$ is zero, so we can not say that any level set that is greater than $\Omega_C$ is a positively invariant set (as it contains the points where $\dot L\ge0$). This metod also applies in higher dimensions, not only in 2D

Answer 2

Let's first start off with LaSalle's Invariance Principle. It says:

Let $X^*$ be an equilibrium point for $X'= F(X)$ and let $L: U \to \mathbb{R}$ be a Liapunov function for $X^*$, where $U$ is an open set containing $X^*$. Let $P \subseteq U$ be a neighborhood of $X^*$ that is closed and bounded. Suppose that $P$ is positively invariant, and that there is no entire solution in $P\setminus\{X^*\}$ on which $L$ is constant. Then $X^*$ is asymptotically stable and $P$ is contained in the basin of attraction of $X^*$.

So basically we have our system $X' = F(X)$ and we have an equilibrium $X^*$ with a closed neighborhood $P$ of that equilibrium. So we just have to check 3 things:

1) $P$ is closed and bounded

2) $P$ is positively invariant

3) $L$ is never constant along any non-equilibrium solution which resides in $P$

If these are satisfied, then we have 2 conclusions:

A) The equilibrium is asymptotically stable

B) The region $P$ is in the basin of attraction

So what they tried to show is that the circle of radius 2 centered at origin is closed and bounded, positively invariant, and $L$ isn't constant along any non-equilibrium solution in the circle.

I'm not entirely convinced of this because the Liapunov function may no longer be strict on the boundary, but I am more confident in saying that the circle of radius 1 centered at the origin is in the basin.

The circle of radius 1 centered at the origin is closed and bounded and since the Liapunov function is strict in this circle, $L$ will not be constant along any non-equilibrium solution curve. Furthermore, our Liapunov function corresponds to the norm of our solution squared (the square of the distance from the origin to a point on the solution). Thus if a solution curve starts inside this circle and later left, it would correspond to an increase in the the distance of the solution from the origin. However, our Liapunov function is strict, so it is strictly decreasing. Therefore, the circle is positively invariant. Now we can apply LaSalle's to conclude the circle of radius 1 centered at the origin is in the basin.

Answer 3

This problem can be handled with an optimization procedure, having in mind that generally is a non convex problem. The result depends on the test Lyapunov function used so we will generalize to a quadratic Lyapunov function

$$ L = p^{\dagger}\cdot M\cdot p = a x^2+b x y + c y^2,\ \ \ p = (x,y)^{\dagger} $$

with $a>0,c>0, a b-b^2 > 0$ to assure positivity on $M$. We will assure a set involving the origin $Q_{\dot L}$ such that $\dot L(Q_{\dot L}) < 0$. The optimization process will be used to guarantee a maximal $Q_{\dot L}$.

After determination of $\dot L = 2 p^{\dagger}\cdot M\cdot f(p)$ we follow with a change of variables

$$ \cases{ x = r\cos\theta\\ y = r\sin\theta } $$

so $\dot L = \dot L(a,b,c,r,\theta)$. The next step is to make a sweep on $\theta$ calculating

$$ S(a,b,c, r)=\{\dot L(a,b,c,r,k\Delta\theta\},\ \ k = 0,\cdots, \frac{2\pi}{\Delta\theta} $$

and then the optimization formulation follows as

$$ \max_{a,b,c,r}r\ \ \ \ \text{s. t.}\ \ \ \ a > 0, c> 0, a c -b^2 > 0, \max S(a,b,c,r) \le -\gamma $$

with $\gamma > 0$ a margin control number.

Follows a MATHEMATICA script which implements this procedure in the present case.

f = {-2 x - y^2, -y - x^2};
L = a x^2 + 2 b x y + c y^2;
dL = Grad[L, {x, y}].f /. {x -> r Cos[t], y -> r Sin[t]};
rest = Max[Table[dL, {t, -Pi, Pi, Pi/30}]] < -0.2;
rests = Join[{rest}, {r > 0, a > 0, c > 0, a c - b^2 > 0}];
sols = NMinimize[Join[{-r}, rests], {a, b, c, r}, Method -> "DifferentialEvolution"]
rest /. sols[[2]]
dL0 = Grad[L, {x, y}].f /. sols[[2]]
L0 = L /. sols[[2]]
r0 = 2.5;
rmax = r /. sols[[2]];
gr0 = StreamPlot[f, {x, -r0, r0}, {y, -r0, r0}];
gr1a = ContourPlot[dL0, {x, -r0, r0}, {y, -r0, r0}, ContourShading -> None, Contours -> 80];
gr1b = ContourPlot[dL0 == 0, {x, -r0, r0}, {y, -r0, r0}, ContourStyle -> Blue];
gr2 = ContourPlot[x^2 + y^2 == rmax^2, {x, -r0, r0}, {y, -r0, r0}, ContourStyle -> {Red, Dashed}];
Show[gr0, gr1a, gr1b, gr2]

Follows a plot showing in black the level sets $Q_{\dot L}$ an in blue the trace of $\dot L = 0$. In dashed red is shown the largest circular set $\delta = 2.03909$ defining the maximum attraction basin for the given test Lyapunov function's family.