1

For which values of $k$ can you prove the following statement? There exists an $n$ such that any planar graph on at least n vertices contains at least $k$ vertices of degree at most $5$. Could it hold for every $k$?

hmakholm left over Monica
  • 291,611
Extra Learn
  • 51
  • Welcome to math.SE! You are more likely to get useful help on this site if you explain what you've tried so far, where you are stuck. Otherwise you are likely to get downvoted or have your question closed. – rogerl Dec 16 '17 at 01:14
  • I can think of one family of planar graphs with $3n$ vertices of degree $6$ and $6$ vertices of degree $2$, so $k>6$ certainly won't work. – hmakholm left over Monica Dec 16 '17 at 01:20
  • ... and of another family with $2n(n-2)$ vertices of degree $6$ and $4$ vertices of degree $3$. – hmakholm left over Monica Dec 16 '17 at 01:29
  • Related: https://math.stackexchange.com/questions/763598/every-planar-graph-has-a-vertex-of-degree-at-most-5 – Jack D'Aurizio Dec 16 '17 at 15:25
  • @HenningMakholm: were you thinking to similar objects? – Jack D'Aurizio Dec 16 '17 at 15:43
  • 1
    There also is a class of planar graphs with $4^n-4$ vertices of degree $6$ and $6$ vertices of degree $4$. – Jack D'Aurizio Dec 16 '17 at 15:57
  • 1
    @JackD'Aurizio: I can't quite discern what's going on a the tips but the tetrahedral example looks like what I was envisaging in my second comment. – hmakholm left over Monica Dec 16 '17 at 16:03
  • 1
    @JackD'Aurizio: Such a tiling can't exist. If we tile a sphere (of Euler characteristic $2$) with $n$ hexagons and $k$ pentagons, meeting in threes at the corners, then we have $\frac13(6n+5k)$ vertices and $\frac12(6n+5k)$ edges. Inserting that into $V-E+F=2$, a bit of algebra produces $k=12$. – hmakholm left over Monica Dec 16 '17 at 17:39
  • 1
    An extension of this argument: Given a planar graph where all faces are triangles, let the "defect" of a vertex be $6$ minus its degree. $V-E+F$ now implies that the total defect must be exactly $12$. Since a vertex in a triangular graph (other than $C_3$) cannot have degree less than $3$, there must be at least $4$ vertices with degree less than $6$. – hmakholm left over Monica Dec 16 '17 at 17:47

1 Answers1

3

Summary: $k=4$ is the largest $k$. We can eliminate $k \leq 2$ using Euler's Formula and the Handshaking Lemma. We can eliminate $k=3$ with some case analysis. And when $k=4$, there's a construction of a family of planar graphs with $n-4$ degree-$6$ vertices and $4$ degree-$3$ vertices.

A graph with $q:=n-k$ vertices of degree $\geq 6$ has at least $\tfrac{1}{2} 6q=3q$ edges, by the Handshaking Lemma. Euler's Formula thus implies that a $n$-vertex planar graph has $3q \leq 3n-6$, or equivalently $q \leq n-2$. This proves $k \geq 2$.

If $k=2$ and the small degrees are $d_1$ and $d_2$, then by bounding the sum of the degrees, we get $$ 6(n-2)+d_1+d_2 \leq 2e \leq 6n-12 $$ which implies $d_1$ and $d_2$ are both $0$. We can delete these two isolated vertices to contradict Euler's Formula. So $k \geq 3$.

If $k=3$ and the small degrees are $d_1$, $d_2$, and $d_3$, then $$6(n-3)+d_1+d_2+d_3 \leq 2e \leq 6n-12.$$ That is, $d_1+d_2+d_3 \leq 6$.

If we have an isolated vertex, we delete it and end up back in the $k=2$ case. If we have a vertex of degree $2$, we can contract it with one of its neighbors, and end up back in the $k=2$ case. Either way, we reach a contradiction.

If we have a vertex of degree $1$ then... If its neighbor has degree other than $6$, than we can delete the degree-$1$ vertex and end up in the $k=2$ or $k=1$ case, reaching a contradiction. Otherwise, we still delete it, but we remain in the $k=3$ case, but with a degree-$5$ vertex, but then we contradict $d_1+d_2+d_3 \leq 6$.

Thus $d_1$, $d_2$, and $d_3$ are all at least $3$, contradicting $d_1+d_2+d_3 \leq 6$.

Hence $k \geq 4$.

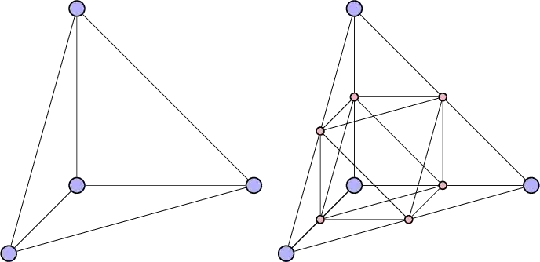
Finally, I think the construction Henning Makholm and Jack D'Aurizio seem to be talking about in the comments is:

  1. Take a tetrahedron,
  2. subdivide each edge once, and
  3. connect newly created vertices that share a face that was on the original tetrahedron.

Then repeat steps 2 and 3. (Projecting onto a sphere or plane as desired.) Here's an attempt at a drawing:

enter image description here

We always create vertices of degree $6$, and we have exactly $4$ vertices of degree $3$. Thus construction implies $k \leq 4$.

Rebecca J. Stones
  • 27,246