What boundary conditions would provide a weak solution to the problem
$\Delta^2u =f$
in the space $H_0^1(U)\cap H^2(U)$?
I'm mostly lost on where to start because I don't understand what the intersection $H_0^1\cap H^2(U)$ would contain. Is $H_0^1(U)$ not contained in $H^2(U)?$
Any help appreciated!
The biharmonic equation takes two boundary conditions. Typical choices:
The first choice, with homogeneous boundary conditions, simply means we look for a solution in $H^2_0(U)$, which is strictly smaller than $H^1_0(U)\cap H^2(U)$. The post Unique weak solution to the biharmonic equation is very relevant here.
The second choice, with homogeneous conditions, leads to $v\in H^1_0(U)$ and subsequently $u\in H^1_0(U)\cap H^3(U)$ which is slightly weird (and also smaller than $H^1_0(U)\cap H^2(U)$).
The only natural situation that I can think of where you get $H^1_0(U)\cap H^2(U)$ is when you prescribe homogeneous Dirichlet and non-homogeneous Neumann condition, $\frac{\partial u}{\partial n}=g$ on $\partial\Omega$. Then one has to require $g$ to be compatible with the desired regularity: there must be some function $w\in H^1_0(U)\cap H^2(U)$ such that $\frac{\partial w}{\partial n}=g$. Writing $u=w+\tilde u$, you then reduce the problem to the homogeneous case: $\tilde u \in H^2_0(U)$ with $\Delta^2 u = f - \Delta^2 w$.
You also asked for an explanation of that intersected function space. The part $H^2$ indicates the interior regularity and says nothing about boundary behavior. The part $H^1_0$ indicates vanishing of $1$st order on the boundary; intuitively, it's $u=0$ but not necessarily $\partial u/\partial n=0$. Recall that $H^k_0(U)$ consists of all limits of smooth compactly supported functions in $H^k(U)$. Being compactly supported means the derivatives of all orders vanish on the boundary. But the "limits of" part is governed by the index $k$ which indicates how much of that vanishing is actually preserved.
Most notably, $u\in H^2_0(U)$ implies $\nabla u\in H^1_0(U)$ while $u\in H^2_0(U)\cap H^1_0(U)$ only implies $\nabla u \in H^1(U)$.
Here is an illustration of these function spaces, with the domain $U$ being the interval $(-1,1)$.
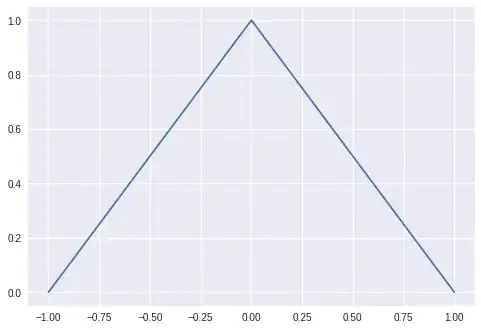
Vanishes on the boundary like $H^1_0$ indicates, but interior smoothness is low.
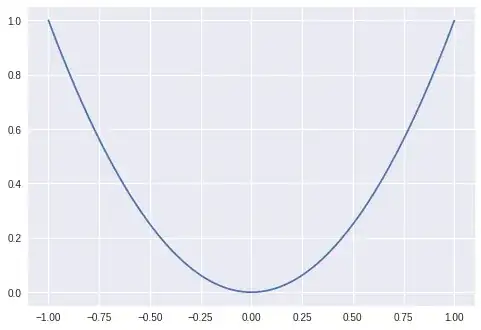
Smooth but no vanishing on the boundary.
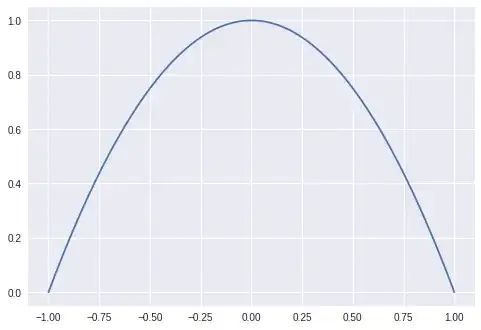
Vanishes on the boundary like $H^1_0$ indicates, and is smooth inside. However, the derivative does not vanish on the boundary: the gradient is not in $H^1_0$.
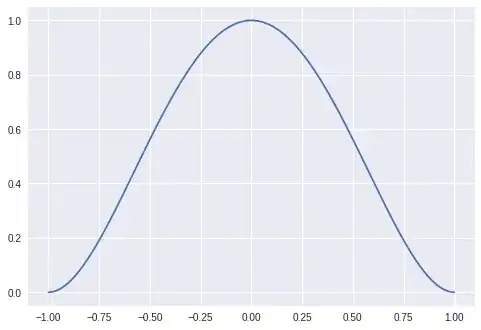
The function is "clamped" on the boundary. I'd say this is a natural space in which to study the biharmonic equation.