6

In $\Bbb R^3$ we have a closed convex polyhedron $P$ with triangularised faces (you may assume it's symmetric about the origin for simplicity.), and a point light source $s\notin P$. Let $F_{1,\cdots, m}$ be all of $P$'s faces, and $\pi_i$ be the plane that passes through $F_i$ respectively. Each $\pi_i$ cuts $\Bbb R^3$ into two open regions one of which contains the interior of $P$ while the other doesn't intersect $P$. For each $i$, we call the open region that doesn't intersect $P$ as $R_i$. Then we know that a face $F_i$ is lighted by $s$ if and only if $s\in R_i$. Now consider the collection $\mathcal F_s$ of all faces that are lighted by $s$.

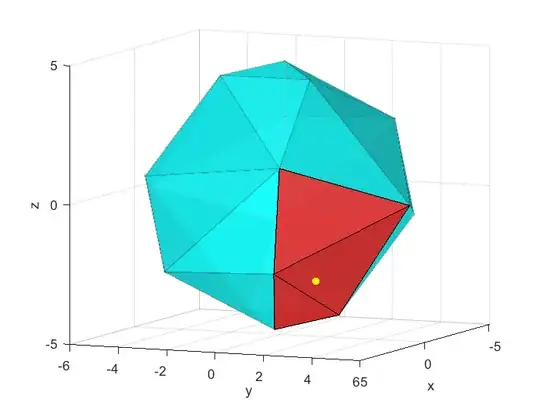
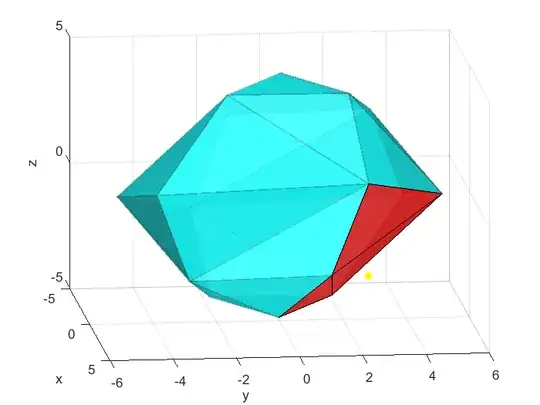
An illustration made in Matlab where the yellow point indicates the light source and faces coloured red are lighted faces (viewed from two different angles): enter image description here enter image description here

I have to show that $\mathcal F_s$ is entirely connected, in the sense that any face in $\mathcal F_s$ must share an edge with at least one another face in $\mathcal F_s$ (which is slightly stronger than path connectedness, because in this case two faces connected only by a single point are not considered as connected), and that the union of all faces in $\mathcal F_s$ is simply connected.

This is geometrically intuitive, but the proof turns out extremely hard for me. Having been working on it for a whole week, I still get virtually nothing of value. Could anybody help?

PS: for what it's worth, it's 2D analog is very easy to prove, because edges of a convex polygon form a loop and we can make sense of a "direction" on it. But in 3D, the connectivity between faces is much more complicated. So I don't think there is an easy extension from 2D to 3D.
Vim
  • 13,905
  • 1
    Related, but much easier: https://math.stackexchange.com/questions/1749730/how-many-faces-of-a-solid-can-one-see/1749751#1749751 – Ethan Bolker Nov 29 '17 at 13:14

1 Answers1

5

Suppose $F$ and $G$ are faces you can see from point $s$. Choose $f \in F$ and $g \in G$ and consider the plane $\pi$ determined by $f$, $g$ and $s$. That plane intersects $P$ in a convex polygon, and the two dimensional argument in $\pi$ implies the intersections with $F$ and $G$ are connected as you wish. Then so are $F$ and $G$.

If the intersection of $\pi$ with $P$ happens to contain a vertex of $P$ just jiggle $f \in F$ a little to make the intersection generic.

Ethan Bolker
  • 103,433
  • Thanks for the information you provided! I'll check them out. – Vim Nov 29 '17 at 13:28
  • Could you elaborate a bit on what do you mean by "...and the two dimensional argument in π implies the intersections with F and G are connected"? – Vim Nov 29 '17 at 15:06
  • 1
    In your question you say you understand how to prove the theorem in two dimensions. So just use that argument on the intersection $P \cap \pi$ in plane $\pi$. This might be clearer if you add $f$, $g$ and $\pi$ to your matlab picture. – Ethan Bolker Nov 29 '17 at 15:14
  • Thanks! It's all clear now! – Vim Nov 29 '17 at 15:36
  • As a followup question (if you might be interested): can we inductively use your argument to prove higher dimensional cases? For example, in 4D, we use an appropriately chosen 3D affine space to cut the convex 4-gon and apply the 3D result on it. And so on. I'm not 100 percent sure there'll not be any pitfall though. – Vim Nov 30 '17 at 02:53
  • Ok there's another argument somebody told me that's directly applicable in $\Bbb R^n$ (using projection central at the $s$ onto a plane separating $s$ and $P$). Never mind. – Vim Nov 30 '17 at 15:35
  • I think my argument will generalize to higher dimensions. But for the sake of completeness on this site, you or your friend should post the other argument here as a second answer. – Ethan Bolker Nov 30 '17 at 15:38
  • sure, when I have time I'll post a detailed version here and let you know. – Vim Nov 30 '17 at 15:40
  • Sorry, it turned out the "directly applicable" argument that somebody told me isn't sufficient. It surely can guarantee simple connectedness, but, without explicitly viewing polyhedral surfaces as manifolds with boundary (of some kind), I don't think it can rule out the "degenerate" contact via lower dimension simplices (single points in $\Bbb R^3$ and $(n-2)$-simplices in $\Bbb R^n$.). Concerning this, your approach is more satisfactory. – Vim Dec 02 '17 at 13:07
  • In order to generalise your arugment to higher dimensions one has to justify how to wisely "jiggle" the subspace (plane) as you stated in your answer. But I didn't find it trivial either. I have simplified the problem to this question, if you might still feel interested. – Vim Dec 03 '17 at 08:00
  • I haven't looked carefully at the new problem. Are you sure you need it? You don't need to be very wise when jiggling. The set of points $f$ such that it together with $g$ and $s$ determine a plane that passes through a vertex of $P$ (or satisfies any other similar special condition) has measure $0$, is nowhere dense, etc. Just pick one in general position. Then the connecting $f$ to $g$ in $P$ in that plane will have to cross generically from facet to facet in $P$. (I think this argument is sound.) – Ethan Bolker Dec 03 '17 at 14:02
  • I'm aware of the fact that planes (their normals actually) that avoid all vertices are nowhere dense, but the difficulty lies exactly in showing that planes connecting $F$ to $G$ are "generic", and what I'm trying to do is to find an open set of normals that meet this requirement, but it wasn't that trivial. – Vim Dec 03 '17 at 14:06