1

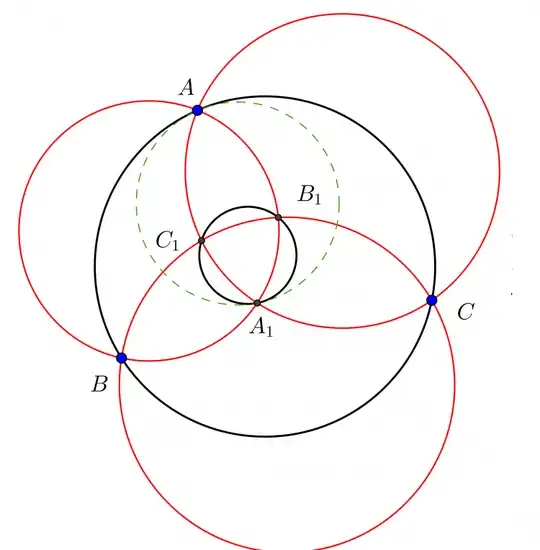
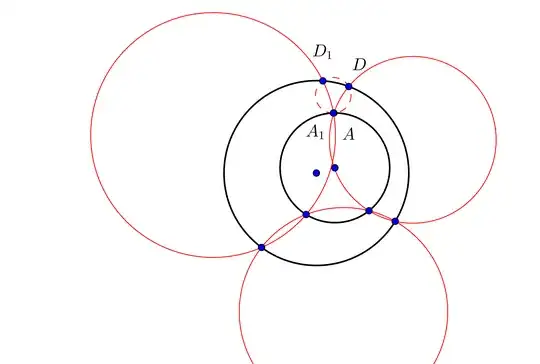
Let six points $A, B, C, A_1, B_1, C_1$ on the plane, such that four points $B, C, B_1, C_1$ lie on a circles, four points $C, A, C_1, A_1$ lie on a circle and four points $A, B, A_1, B_1$ lie on a circle. I am looking find a proof that:

enter image description here

Exist a circle tangent to $(ABC)$, $(A_1B_1C_1)$ at two points $A, A_1$ respectively.

Cố Gắng Lên
  • 333

2 Answers2

2

This does sound like a special case of Miquel's six circle theorem.

Miquel's theorem

Add another point $D$ on the outer circle. Then $\bigcirc CDC_1$ will intersect $\bigcirc A_1B_1C_1$ in a point $D_1$. Miquel's theorem guarantees that $ADA_1D_1$ are cocircular. As you move $D$ towards $A$, $D_1$ will move towards $A_1$. In the limit, $A=D$, $A_1=D_1$ and the two blue circles coincide. In this situation, the dashed circle has a double point with both of the black circles, so it is tangent to them.

Use this interactive version (created using CindyJS) to experience the limit process yourself.

MvG
  • 44,006
  • How can application Miquel's six circle theorem to show $ADA_1D_1$ are concyclic? – Cố Gắng Lên Nov 27 '17 at 16:34
  • @CốGắngLên: If you follow the description on the Wikipedia page I linked to, then their $A,B,C,D$ are your $B,C,B_1,C_1$ and their $W,X,Y,Z$ are your $A,D,A_1,D_1$. So the application of the theorem is pretty much straight forward. Proving the theorem would be a different question, probably worth asking. – MvG Nov 27 '17 at 16:52
  • Can You help me show which is the first circle, second circle, third circle....in this configuration? – Cố Gắng Lên Nov 27 '17 at 16:56
  • @CốGắngLên: Traditionally you start with one circle, which would be $\bigcirc BCB_1C_1$, and then in the end conclude a cocircularity in a circle that has no points in common with that first circle, i.e. $\bigcirc ADA_1D_1$ here. So these are first and sixth circle, and the others are second through fifth, in no particular order. But the configuration is so highly symmetric that it makes little difference which circle is which: as long as the overall combinatorics is as the theorem has it, any of the six cocircularities is the consequence of the other five. – MvG Nov 27 '17 at 17:56
  • @CốGắngLên: I just posted a question asking for proofs of Miquel's theorem, and providing one such proof myself. – MvG Nov 27 '17 at 22:10
  • I understand your proof now. Thank You – Cố Gắng Lên Nov 28 '17 at 16:33
0

enter image description here This Figure Miquel's six circle cofiguration we move $A_1$ towards limit to $A$ but $D_1$ don't move limit to $D$

Cố Gắng Lên
  • 333
  • This looks like a comment to my post, not an independent answer. But my limit process was $D\to A,D_1\to A_1$, not $A_1\to A,D_1\to D$ as this answer suggests. I suggest you delete this post, and perhaps add a comment to my post. You can copy an image URL from a post draft to a comment to include an image without ever publishing the draft. You can also copy the URL from the image in this post, in case it is still relevant. – MvG Nov 29 '17 at 12:31