I was recently asked to sketch $(x^2-2)^2+(y^2-2)^2=2$, which did not prove to be too problematic, for establishing the range and domain of the expression gives nearly all of it away.
I then asked myself what would happen as I change the constant on the R.H.S. I recommend you try this yourself:
https://www.desmos.com/calculator/tlksmrpzxu
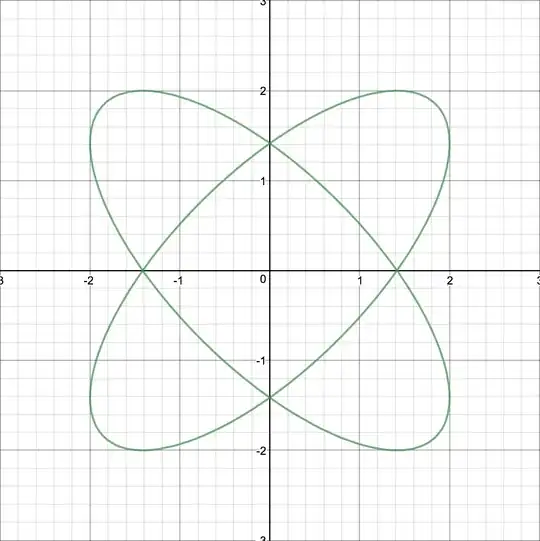
The constant that stood out as yielding the most intriguing result is $4$. The graph looks like this:
I then wondered how on earth I could deduce this just by analysing $(x^2-2)^2+(y^2-2)^2=4$.
One of my approaches involved spotting that the two 'orbits' are in the shape of ellipses with equations (derived partly experimentally, partly using the ellipse formula) $x^2-xy\sqrt{2}+y^2=2$ and $x^2+xy\sqrt{2}+y^2=2$. Can I derive these just from $(x^2-2)^2+(y^2-2)^2=4$?