Why is TREE(3) not infinite?

Question

this is my first ever question on this forum so bear with me if the formatting or phrasing of the question itself seems strange...

I was reading about TREE(3) and the rules followed in generating the sequence of trees here:

https://cp4space.wordpress.com/2012/12/19/fast-growing-2/

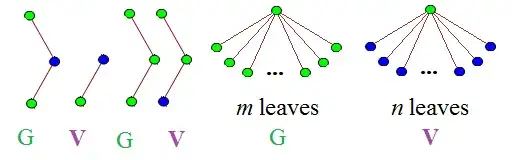
Midway through the article when describing a hypothetical game in which the trees are being generated, a lower bound for X is presented and, therefore, m and n have an upper bound.

"After this incredibly long sequence of moves, the next six moves might be these (let m and n be positive integers where m + n < x; in practice, x is so large that it is unrestrictive):"

My question is what rule in creating the sequence says that X needs to be bounded at all? Why can't either player play a tree with an infinite number of leaves?

I am not a math major, I just came across the topic in a Numberphile video and wanted to understand more.

Thanks

Answer 1

The rule is that on the $k^{\text{th}}$ turn, you're not allowed to play a tree with more than $k$ nodes. (In particular, you're never allowed to play an infinitely large tree.)

The reduction to Chomp requires players to be able to play trees with up to $m+n$ nodes. So if you want to play $1000 \times 2000$ Chomp, for instance, you can't play the six moves

and then start playing Chomp right away: you have to do $3000$ or so time-wasting moves that let the TREE game advance to the point where you can play trees that big.

In the blog post, one possible very long sequence that doesn't interfere with Chomp is provided. So to play $1000 \times 2000$ Chomp, you could begin with the first $3000$ moves of that sequence, then with the six moves above (with $m=1000$ and $n=2000$), and then finishing the game is isomorphic to Chomp on a $1000 \times 2000$ board.

Note that, although "$x$ is so large that it is unrestrictive", it is not so unrestrictive that we can play any Chomp variant. For example, you would not be able to simulate Chomp on a $\text{TREE}(3) \times \text{TREE}(3)$ board in the TREE game.

(Not only can you not do it with this approach to simulating Chomp, but you can't do it with any approach, since Chomp on a $\text{TREE}(3) \times \text{TREE}(3)$ board can have games longer than $\text{TREE}(3)$, and the TREE game by definition cannot.)