9

Every knot and link can be untied if you allow it to pass through itself. (This is why the unknotting number is always finite.) This changes if you only allow each component of the link to pass through itself, prohibiting them from passing through any other component. The Whitehead link can be untied that way: the central crossing only involves one component, and flipping it unties the link. The Hopf link, on the other hand, cannot. This is because it has linking number $\pm1$ (depending on the relative orientations of the two components), and the linking number doesn't change when a component passes through itself.

Can the Borromean rings be unlinked if we allow each component to pass through itself? The above argument with the linking number doesn't work anymore, since the linking number between any two components is $0$.

Akiva Weinberger
  • 25,412

1 Answers1

4

The Borromean rings are not link homotopic to the three component unlink, that is, one cannot transform the Borromean rings into the three component unlink by a deformation that allows components to pass through themselves, but does not allow one component to pass through another. One can use Milnor invariants to show this. Milnor's original work was part of his PhD thesis. I will use a formulation that can be found in this paper of Mellor and Melvin.

For a three component link, a complete invariant of link homotopy is given by the three pairwise linking numbers $p$, $q$, and $r$, and another residue class $\mu$ modulo the greatest common divisor of $p$, $q$, and $r$. The Borromean rings have $p=q=r=0$, but $\mu=\pm 1$ (depending on how one orients the link). The unlink has $p=q=r=\mu=0$, and so the Borromean rings are not link homotopic to the three component unlink.

The residue class $\mu$ is defined as follows. Let $X$, $Y$, and $Z$ be longitudes of the three components of the link, and let $F_X$, $F_Y$, and $F_Z$ be the corresponding Seifert surfaces of the components of $L$. Define $w_X$ to be a word in $y$ and $z$ as follows. Start at some point on $X$ and traverse the longitude once. Each time one passes through the Seifert surface $F_Y$, append either $y$ or $y^{-1}$ to $w_X$ depending on the orientation of the intersection. Similarly, append $z$ or $z^{-1}$ each time one passes through the Seifert surface $F_Z$. Define $m_{X}$ to be a signed count of the following patterns in $w_X$:

  • ($y\dots z$): An instance of $y$ followed eventually by $z$ increases $m_X$ by one.
  • ($y^{-1}\dots z^{-1}$): An instance of $y^{-1}$ followed eventually by $z^{-1}$ increases $m_X$ by one.
  • ($y \dots z^{-1}$): An instance of $y$ followed eventually by $z^{-1}$ decreases $m_X$ by one.
  • ($y^{-1}\dots z$): An instance of $y^{-1}$ followed eventually by $z$ decreases $m_X$ by one.

Similarly define $m_Y$ and $m_Z$. Let $t$ be the signed count of the number of triple points among the three Seifert surface $F_X$, $F_Y$, and $F_Z$. Then $$\mu = m_X + m_Y + m_Z - t \mod \gcd(p,q,r).$$

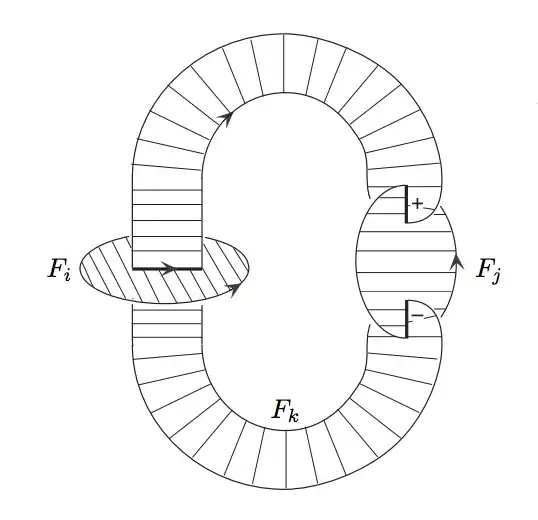
enter image description here

The picture of the Borromean rings above is taken from the Mellor and Melvin paper. Let $F_X=F_i$, $F_Y=F_j$, and $F_Z=F_k$. Then $m_X=1$, $m_Y=m_Z=0$, and there are no triple points so $t=0$. Hence for the Borromean rings with the depicted orientation, $\mu=1$. Thus the Borromean rings are not link homotopic to the three component unlink.

Adam Lowrance
  • 3,543
  • 1
  • 16
  • 20