Inequality with power and logarithm

Question

inspired by this: show this inequality $\left(\sum_{i=1}^{n}x_{i}+n\right)^n\ge \left(\prod_{i=1}^{n}x_{i}\right)\left(\sum_{i=1}^{n}\frac{1}{x_{i}}+n\right)^n$ I propose to you this inequality for all $x>0$ and $x\neq 1$: $$(\frac{ln(x)+2n}{2n-1+x})^n<\frac{1}{x}$$

Edit :I make a mistake (maybe I'm lucky) but the inequality above is not the inequality I want to solve , the inequality that I want to prove is here :$$\forall x>0, \forall n\in N^*,\quad (\frac{-ln(x)+2n}{2n-1+x})^n\leq\frac{1}{x}$$

I can prove this like everyone for very small $n$ but the general case evade to me .

Thanks a lot .

Answer 1

In order to avoid non-integer powers of negative numbers, I consider the inequality only for natural $n$. Put $x=y^n$. Since for $y\ge e^2$ the inequality follows from Piquito’s comment, we assume that $y\le e^2$. A simplification transforms the inequality to $f(y)=y^n+ny\ln y-2ny+2n-1>0.$ It is easy to check that when $y$ tends to the infinity, $f(y)$ tends to the infinity too and when $y$ tends to the zero, $f(y)$ tends to $2n-1$. Thus the set $K=\{y\in\Bbb R: f(y)\le 0\}$ is bounded. It is easy to check that $1\in K$. Since the function $f$ is continuous, the set $K$ is closed. So the set $K$ is compact and the function $f$ attains its minimum at some point $y_0\in K$. Since the function $f$ is differentiable, $f’(y_0)=0$. It is easy to check that $f’(1)=0$ and $f(1)=0$. Since $f’’(y)=n((n-1)y^{n-2}+y^{-1})>0$, the equation $f’(y)=0$ has only one solution. Thus the function $f$ attains its minimum in the unique point $y_0=1$.

Answer 2

Proof

Lemma 1: For $x>1,\quad\left(\frac{-\ln x+2n}{2n-1+x}\right)^n < \left(\frac{-\left(1-\frac{1}{x}\right)+2n}{(2n-1+x)}\right)^n$

Proof, where the first step is proven here:

$$\begin{aligned} \ln x &> 1-\frac1x;& x>1 \\ -\ln x+2n &< -\left(1-\frac{1}{x}\right)+2n \\ \left(\frac{-\ln x+2n}{2n-1+x}\right)^n &< \left(\frac{-\left(1-\frac{1}{x}\right)+2n}{(2n-1+x)}\right)^n;& (2n-1+x)>0 \end{aligned}$$

---

Lemma 2: For $n>1,t>1,\quad{\frac{t}{t^n}+2nt-(t^n+t)}<2n-1$

Proof, where the first assumption can be proven by induction:

$$\begin{aligned}t^{n}&>t\left(\frac{1}{t^n}+(2n-1)\right)-(2n-1);& n>1, t>1 \\ t^{n}+t&>t\left(\frac{1}{t^n}+2n\right)-(2n-1) \\ -t^{n}-t&<-t\left(\frac{1}{t^n}+2n\right)+(2n-1) \\ {\frac{t}{t^n}+2nt-(t^n+t)}&<2n-1 \end{aligned}$$

---

Lemma 3: For $n>1,x>1,\quad\left(\frac{{-(1-\frac1x)+2n}}{2n-1+x}\right)^n<\frac{1}x$

Using lemma 2, with the substitution $x=t^n$,

$$\begin{aligned} {\frac{x^{1/n}}{x}+2nx^{1/n}-(x+x^{1/n})}&<2n-1 \\ x^{1/n}\left({\frac1x+2n-1}\right)&<{2n-1+x} \\ x\left({\frac1x+2n-1}\right)^n&<\left(2n-1+x\right)^n \\ \frac{\left({\frac1x+2n-1}\right)^n}{\left(2n-1+x\right)^n}&<\frac{1}x;&{\left(2n-1+x\right)^n}>0 \\ \left(\frac{{-(1-\frac1x)+2n}}{2n-1+x}\right)^n&<\frac{1}x \end{aligned}$$

Combining lemma 1 and lemma 3, we have $\left(\frac{-\ln x+2n}{2n-1+x}\right)^n<\left(\frac{{-(1-\frac1x)+2n}}{2n-1+x}\right)^n<\frac{1}x$, as desired.

---

Addendum

We can create the sharper bound, for sufficiently small $x>1$, $\left(\frac{-\ln x+2n}{2n-1+x}\right)^n < e^{(1-x^2)/(2x)}<\frac1x$. The reason $x$ must be small is because the inequality reverses for sufficiently large $x$. The inequality can be found by using the substitution $u=1-2n$ and observing:

$$\left(\frac{-\left(1-\frac{1}{x}\right)+2n}{(2n-1+x)}\right)^n=\underbrace{\left[\frac{\left(1-\frac{x}{u}\right)^u}{\left(1-\frac{1/x}{u}\right)^u}\right]^{1/2}}_a \underbrace{\left[\frac{1-\frac{x}{u}}{1-\frac{1/x}{u}}\right]^{-1/2}}_b$$

As $n\to +\infty$, $a$ approaches $\left(\frac{e^{-x}}{e^{-1/x}}\right)^{1/2}=e^{(1-x^2)/(2x)}$, while $b$ approaches $1$.

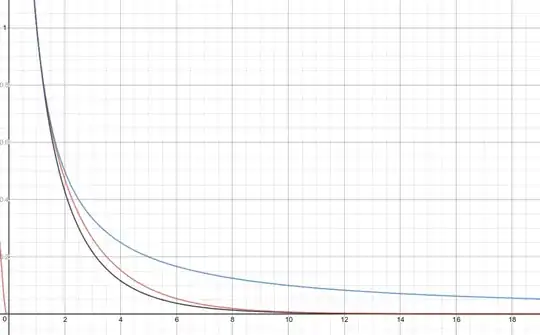
As shown in the figure below, the red curve, $e^{(1-x^2)/(2x)}$, forms a closer bound of the black curve, $\left(\frac{-\ln x+2n}{(2n-1+x)}\right)^n;\quad n=20$, than the blue curve, $\frac1x$. However, the inequality reverses around $x>14.3$.