0

enter image description here

It's been driving me bonkers. As it's a contradiction proof I assume that there's a rational solution for the above equation. Then my prof told me to set the equation equals $0$, then sub in $p\over{q}$ for $x$, with $p$ in the set of integers and $q$ in the set of natural numbers, $ p ,q$ have no common factors, then factor everything by $q^4$, giving the equation [![enter image description here][2]][2]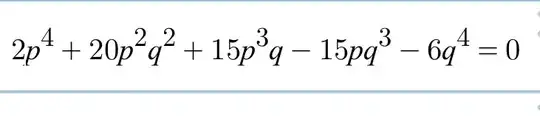enter image description here

Then I should use the fact that $2p^4 +6q^4$ isn't divisible by $5$, which means that those two terms will never subtract the other three terms in such a way that they all equal $0$, thus proving there's no rational solution.

I've checked it as a graph on Desmos and the proposition appears correct. However I'm at an utter lost for how to prove $2p^4 +6q^4$ isn't divisible by $5$ to proceed. I'm utterly lost and have scratched out so many failed attempts.

DynamoBlaze
  • 2,975
Long Vuong
  • 528

1 Answers1

1

HINT

If n is not divisible by $5$, then $n^4 \equiv 1 (mod 5)$

Bram28
  • 103,721
  • As surprising as this might sound, we haven't covered modular arithmetic(?) yet. But even after looking up what 1(mod5) means (1 right?) I don't get the hint. – Long Vuong Oct 27 '17 at 03:16
  • Also, where did n come from? – Long Vuong Oct 27 '17 at 03:19
  • 1
    $a\equiv b\pmod{k}$ is defined as meaning that $a-b$ is a multiple of $k$. $n^4\equiv 1\pmod{5}$ means that $n^4$ is always one more than a multiple of five. As $5$ is the same thing as zero modulo five, and so are any other multiples of five, the above equation simplifies to be $2\cdot\color{red}{1}+0+0-0-6\cdot\color{red}{1}\equiv 0\pmod{5}$ where the red ones are a direct result of the hint. – JMoravitz Oct 27 '17 at 03:19
  • So now I have to ask where did n come from, why can you set $n^4\equiv 1\pmod{5}$, and how does this all prove that there doesn't exist some p and q such that $p^4$ + $q^4$ doesn't equal 5 or some multiples? – Long Vuong Oct 27 '17 at 03:34
  • You can prove that $n^4\equiv 1\pmod{5}$ for every $n\not\equiv 0\pmod{5}$ by casework. This proves that $p^4+q^4\not\equiv 0\pmod{5}$ for $p$ and $q$ not simultaneously multiples of five again by casework (they can only add to be $1$ or $2$ mod 5). $n$ here was just selected as a placeholder so that the statement could be made generally and could be seen to apply to both $p^4$ and to $q^4$. – JMoravitz Oct 27 '17 at 03:36
  • @LtotheV Sorry I was offline for a while ... I feel JMoravitz gave perfectly good answers to your questions though ... are you still working on this? Here are some proofs of the result that $n^4 \equiv 1$ for $n$ not divisible by $5$ by the way. With modular arithmetic these are easiest, but with basic algebra you can see this as well. – Bram28 Oct 27 '17 at 15:47
  • @JMoravitz Thanks for answering the OP's questions here! – Bram28 Oct 27 '17 at 15:47