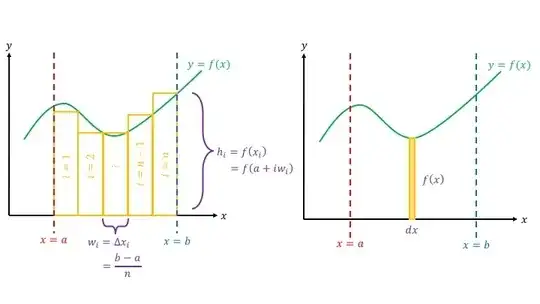
Riemann integrals of the form $\int f(x)\,dx$ with respect to a single variable are pretty simple; they work like this:
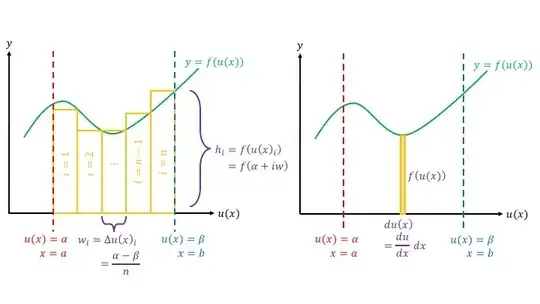
Sometimes, integrals take the form $\int f(u(x))\,d(u(x))$ where $u$ is another function—but these aren’t too different either:
To be explicit, one has the transformation $$\int f(u(x)\,d(u(x)) = \int f(u(x)) \, \frac{du}{dx} \, dx$$
Is this how integrals with respect to measures, of the form $\int f(x)\,d\mu(x)$ or the like, are evaluated?
I have tried researching basic measure theory for many days, but it seems pretty convoluted when broaching the topic of integrals. Hopefully I will be getting a book on measure theory and integration soon. In the mean time, I would appreciate it if anyone could shed some light on how measures are involved in the computation of integrals.