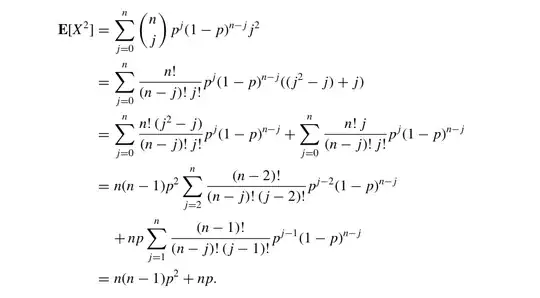The first step in calculating the variance of a Binomial Random Variable is calculating the second moment.
I have no idea as to how the last two steps have happened. Why is a n(n-1)p^2 outside the first summation and a similar expression outside the second? Also, how did the expression turn out to be the last equation?
First term is obtained as follows:
\begin{align} \sum_{j=0}^{n} \frac{n!(j^2-j)}{(n-j)!j!}p^j(1-p)^{n-j} &= \sum_{j=2}^{n} \frac{n!(j^2-j)}{(n-j)!j!}p^j(1-p)^{n-j}\tag{1}\\&=\sum_{j=2}^{n} \frac{n!(j(j-1))}{(n-j)!j!}p^j(1-p)^{n-j} \tag{2}\\ &= \sum_{j=2}^{n} \frac{n!}{(n-j)!(j-2)!}p^j(1-p)^{n-j} \tag{3} \\ &= n(n-1)\sum_{j=2}^{n} \frac{(n-2)!}{(n-j)!(j-2)!}p^j(1-p)^{n-j} \tag{4}\\ &= n(n-1)p^2\sum_{j=2}^{n} \frac{(n-2)!}{(n-j)!(j-2)!}p^{j-2}(1-p)^{n-j} \tag{5} \\ &= n(n-1)p^2\sum_{j'=0}^{n-2} \frac{(n-2)!}{(n-2-j')!(j')!}p^{j'}(1-p)^{n-2-j'} \tag{6} \\ &= n(n-1)p^2 \tag{7} \\ \end{align}
where equation $(1)$ is due to $j^2-j=0$ if $j=0$ or $j=1$, hence we can start summing from $2$ rather than $0$.
Equation $(2)$ is just $j^2-j=j(j-1)$.
Equation $(3)$ is due to $j!=(j-2)!j(j-1)$
Equation $(4)$ is due to $n!=(n-2)!n(n-1)$.
Equation $(5)$ is just factorize $p^2$ outside.
Equation $(6)$ is a change of variable of $j'=j-2$
To obtain equation $(7)$, notice that in equation $(6)$, the term inside the sum if the pmf of binomial distribution with parameter $n-2$ and $p$.
I will leave the second term as an exercise.
The $n$ and $n-1$ are coming out of the $n!$ remember that $n!=n*(n-1)*(n-2)!$. The $p^2$ came from the $p^j$ since $p^j=p^{j-2}*p^2$. Once this terms are out both sums (separately) are equal to the probability mass function of a binomial random variable hence they sum to 1. Hence the result.
They distributed out constant factors from series so that a change of variables would make it the series of probabilities for a binomial expansion $(p+1-p)^{n-1}$. They did not show their work, thinking it would be obvious. Clearly it is not.
I'll just do one of the terms $${ \quad \sum_{j=0}^n\dfrac{n!\ j}{(n-j)!\ j!}p^j(1-p)^{n-j} \\ = \sum_{j=0}^n \dfrac{n(n-1)!\,j}{(n-1-j+1)!\, j\, (j-1)!} p\, p^{j-1}(1-p)^{n-1-j+1} \\ = np \sum_{j=0}^n\dfrac{(n-1)!}{(n-1-(j-1))!\,(j-1)!}p^{j-1}(1-p)^{n-1-(j-1)} \\ = np \sum_{j-1=-1}^{n-1}\binom{n-1}{j-1}p^{j-1}(1-p)^{n-1-(j-1)} \\ = np \sum_{j-1=0}^{n-1}\binom{n-1}{j-1}p^{j-1}(1-p)^{n-1-(j-1)} \\ = np \sum_{k=0}^{n-1}\binom{n-1}k p^k(1-p)^{n-1-k} \\ = np (p+(1-p))^{n-1} \\ = np }$$
The other term follows likewise. Of particular note we use the conveniention that $\binom{r}{-1}=0$.
$$\mathrm{Var}[X] = \mathbb E\left[X^2\right] - \mathbb E[X]^2,$$
where $\mathbb E[X] = np$ and $\mathrm{Var}[X] = np(1-p)$. So
$$\mathbb E\left[X^2\right] = \mathrm{Var}[X] + \mathbb E[X]^2= np(1-p) +(np)^2=np(1-p+np)= n(n-1)p^2 + np$$
Let $Y_i \overset {\text{i.i.d.}} \sim \mathrm{Bern}(p)$, then
$$\mathbb E[X] = \mathbb E\left[\sum_{i=1}^n Y_i\right] = \sum_{i=1}^n \mathbb E[Y_1] = np$$
$$\mathrm{Var}[X] = \mathrm{Var} \left[\sum_{i=1}^n Y_i\right] \overset {Y_i\text{ i.i.d.}} = n \:\mathrm{Var}[Y_1] = np(1-p),$$
as $\text{Var}[Y_1]= p - p^2$:
$$\mathbb E[Y_1^2] = 1^2 \cdot p + 0^2 \cdot (1-p) = p=\mathbb E[Y_1]$$
The Momentgenterating Funktion (MGF) of a RV X is defined as:
$$M(t) =\mathbb E[e^{tX}]$$
It is easy to show that for $Y_i$ $\text{i.i.d.}$ and $X:=\sum_{i=1}^n Y_i$
$$M_X(t) =\mathbb E[e^{tX}]= \mathbb E[e^{tY_1}]^n$$
So for $Y_i \overset{\text{ i.i.d.}}{\sim} \mathrm{Bern}(p)$ we have:
$$M_Y(t)=\mathbb E[e^{tY_1}] = p e^{t} + (1-p)$$
$$\implies M_X(t)= [p e^{t} + 1-p]^n$$
Now the $n$-th moment is the $n$-th derivation of $M(t)$ evaluated at $t=0$ (verify this fact by using the Taylor-series expansion of the exponential function $\exp(tX) = \sum_{n=1}^\infty \frac {t^nX^n} {n!}$), so:
$$M'(t)= n[p e^{t} + 1-p]^{n-1} p e^{t} \implies M'(0) = n[p e^{0} + 1-p]^{n-1} p = np =\mathbb E[X]$$ (works)
$$M''(t)= n(n-1)p^2[p e^{t} + 1-p]^{n-2} e^{t} + M'(t)\implies M''(0) = n(n-1)p^2 + np = \mathbb E[X^2]$$ (also works)
$\dots$
You see, now you have a pattern for all moments, and you didn't even need to solve complicated binomial coefficients ;-)
(Thanks to @Egor Ivanov for caring about my Tex-Skills <3, your edit was lost upon updating this post...)
You can write $X=\sum_{i=1}^n X_i$, where $X_i$ are iid Bernoulli random variables with parameter $p$. Now,
$$ \begin{split} E[X^2] &= E\left[\sum_{i=1}^n\sum_{j=1}^n X_i X_j\right] = \sum_{i=1}^n\sum_{j=1}^nE[X_i X_j] = \sum_{i=1}^nE[X_i^2] + \sum_{i=1}^n\sum_{j=1,j\ne i}^nE[X_i X_j]\\ & = np + n(n-1)p^2, \end{split} $$ where we have used the fact that $E[X_i^2] = E[X_i] = p$ and $E[X_i X_j] = E[X_i]E[X_j] = p^2$ for any pair of distinct indices $(i,j)$.
