1

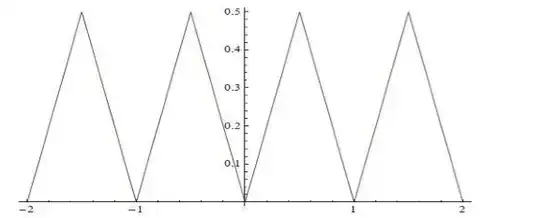
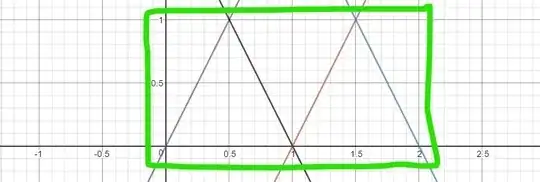
From how I understood the question and judging from solutions I've been provided with (see graph below),

enter image description here

$f(x)$ starts from an x-position, which should be an integer, and assuming this goes on for all integers until infinity.

I also assume the graph follows the function $f(x)=x$, whereby $0\le y \le 0.5$ to make sure the function returns to the nearest integer.

If not, can $f(x)$ be equal to any function as long as it occupies the distance from $x$ to the next integer? For example, $f(x)=2x$ whereby $0\le y \le 1$

enter image description here

And can we say the critical points are all integers? Or maybe I did not understand the question well.

axelmukwena
  • 189

2 Answers2

1

Your first graph is the correct one for $f(x)$, and $f$ is well-defined by the definition in your title--although I might rather say "...to a nearest integer" since more than one could be "nearest."

You are correct that all integers are critical points of $f$. Those are the bottom corners in your graph. However, you missed some critical points, the ones halfway between two consecutive integers--i.e. the values $n+\frac 12$ where $n$ is an integer. Those are the top corners in your graph.

All other points have a derivative of $1$ or $-1$, so we have found all the critical points of $f$.

Rory Daulton
  • 32,888
  • 6
  • 47
  • 64
  • what is the difference between $f$ and $f(x)$, in this context? Is there a difference? And why is the second graph wrong when all graphs produce the same critical points? – axelmukwena Oct 15 '17 at 11:10
  • 2
    @Axel: Strictly, $f$ is the function, while $f(x)$ is a real number, the value of that function for the given domain value $x$. This distinction is often abused and is not significant here. (I see I used them wrongly in my first usage.) The first graph says that $f(0.5)=0.5$ while the first says $f(0.5)=1$. The first is correct, since the nearest integers to $0.5$ are $0$ and $1$ which are each at a distance of $0.5$. The two graphs have the same critical points but only the first is the correct graph. – Rory Daulton Oct 15 '17 at 11:20
0

Notice that $f$ is defined as:

$$f(x):=\begin{cases}n-x\quad \text{if }\ n-\frac{1}{2}\leq x<n\\ x-n\quad \text{if }\ n\leq x<n+\frac{1}{2}\end{cases}$$ for every integer $n$. Now,

$$\lim_{h\,\to\,0^-}\frac{f(n+h)-f(n)}{h}=\lim_{h\,\to\,0^-}\frac{n-(n+h)}{h}=-1$$ and you can show that the right-hand limit is 1. Therefore, derivatives don't exist at $n\in\mathbb{Z}$ $\Big($neither at $n+\frac{1}{2}\Big)$. So now everything depends on your definition of critical point.

moqui
  • 1,421
  • 7
  • 21