Hankel matrix of Catalan numbers

Question

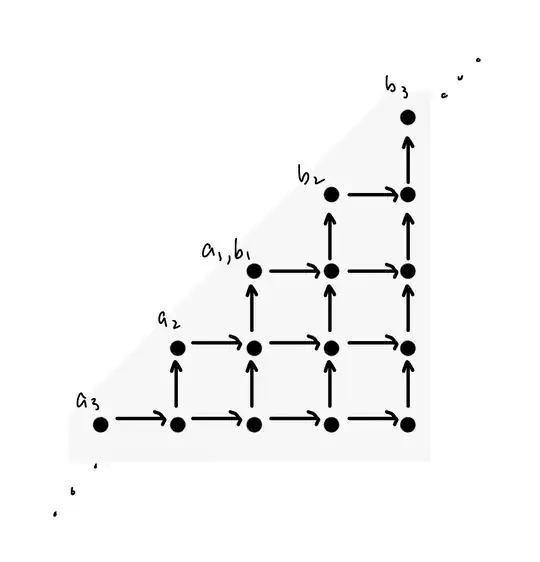
Recall that the $n$-th Catalan number $C_n=\frac{1}{n+1}{2n\choose n}$ counts the number of paths connecting $(0, 0)$ to $(n, n)$ that travel along the grid of integer lattice points of $R^2$ where each path moves up or right in one-unit steps and no path extends above the line $y = x$.

In linear algebra, a Hankel matrix of Catalan numbers is defined as following: $$H_n^t=(C_{i+j+t})_{0\leq i,j\leq n-1}= \begin{bmatrix} c_{t} & c_{t+1} & c_{t+2} & \dots & c_{t+n-1} \\ c_{t+1} & c_{t+2} & c_{t+3} & \dots & c_{t+n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ c_{t+n-1} & c_{t+n} & c_{t+n+1} & \dots & c_{t+2n-2} \end{bmatrix} $$

How can I calculate the Hankel determinant of Catalan numbers for $t=1$?

Is it possible obtain the Hankel determinant of Catalan numbers for $t>1$?

Answer 1

Following Angina Seng's suggestion, let $G$ be the following locally finite, directed acyclic graph:

Let $a_1, \ldots, a_n, b_1, \ldots, b_n$ be as labeled, and let the weight of each edge be $1$. Then $M$ as defined in the Wikipedia article for the Lindström-Gessel-Viennot Lemma is exactly $H_n := H^0_n$, since $M_{i,j}$ is exactly the number of paths connecting $a_i$ to $b_j$, a "staircase" of height $i + j - 2$.

The LGV Lemma is that the determinant of $M$ is given by the following formula:

$$\sum_{P: A \rightarrow B} \text{sign}(\sigma (P))\prod_{P_i \in P} \omega(P_i)$$

where the sum is taken over all families of non-intersecting paths $P = \{P_i\}_{i = 1}^n$ taking the vertices $\{a_1,\ldots,a_n\}$ to the vertices $\{b_1,\ldots,b_n\}$ in some order, $\sigma(P)$ denotes the sign of the permutation of $\{1,\ldots,n\}$ taking $i$ to the index of the end vertex of the path starting at $a_i$, and $\omega(P_i)$ denotes the product of the weights of the edges in the path $P_i$.

It's clear that the only possible family of non-intersecting paths is the one taking each $a_k$ to $b_k$, so the sum has only one term, for which $\sigma(P)$ is the identity, so $\text{sign}(\sigma(P)) = 1$. Furthermore, the weight of every edge was defined to be $1$, so the product of $\omega(P_i)$ is also simply $1$.

So $\det(H^0_n) = \det(M) = 1$ for all $n$. By shifting all the $a_i$ down one diagonal, the same argument applies verbatim, so $\det(H^1_n)$ is also $1$ for all $n$. When $t > 1$ the argument starts to fail because there will exist more than one family of non-intersecting paths connecting $\{a_1,\ldots,a_n\}$ to $\{b_1,\ldots,b_n\}$. (But $\sigma(P)$ will always be the identity, for whatever that's worth.)

Answer 2

The question is about calculating the Hankel determinants $$ H_{n,t}(a) := \det(a_{i+j+t})_{0\leq i,j\leq n-1} $$ where $\,a_n = C_n\,$ is the Catalan numbers OEIS A000108. It is well known that $\,H_{n,0}(a) = H_{n,1}(a) = 1\,$ if and only if $\,a = C.\,$ Less well known is that $\,H_{n,2}(C) = n+1.\,$ I conjecture that the formula is $$ H_{n,t}(C) = h_n(t)/h_0(t) $$ where $$ h_n(t) := \prod_{k=1}^{t-1} (n+k)^{\min(t-k,k)} \prod_{k=1}^{t-2} (2n+2k+1)^{\min(t-1-k,k)}. $$ For example, $$ H_{n,3} = \frac{(n+1)(n+2)(2n+3)}6, \;\; H_{n,4} = \frac{(n+1)(n+2)^2(n+3)(2n+3)(2n+5)}{180}. $$ I wrote Mathematica code to test the conjecture

ClearAll[Cn, h, H, ht, htn, n];
(* Cn[n] is Catalan number C_n )
Cn[n_Integer] := Binomial[2n, n]/(n+1);
(* H[t,n,a] is n X n Hankel matrix using a_t, a_{t+1}, ... )
H[t_, n_Integer, a_] := Table[ a[i+j+t], {i, 0, n-1}, {j, 0, n-1}];
( h[t,n,a] is Hankel determinant H_{n,t} )
h[t_, n_Integer, a_] := If[n<1, Boole[n==0], Det[ H[t, n, a]]];
( ht[t,n] is h_n(t) product )
ht[t_Integer, n_: 0] := Product[(n+k)^Min[t-k, k], {k, 1, t-1}] 
   Product[ (2n+2k+1)^Min[t-1-k, k], {k, 1, t-2}]; 
(* htn[t,n] is conjectured formula for H_{n,t}(C) *)
htn[t_Integer, n_] := ht[t, n]/ht[t];
(* Verify conjecture for a few values of t and n )
And@@Flatten[Table[ htn[t,n] == h[t,n,Cn], {t,1,9}, {n,1,9}], 1]
( True *)