Consider the following equation of real $n\times n$ matrices $$C=\underbrace{DM_S}_{A}+\underbrace{DM_A}_B,$$ where $D$ is diagonal and either positive or negative definite, and where $M_S$ is any symmetric matrix and $M_A$ is any anti-symmetric matrix.
We can prove that the eigenvalues of $A$ lie on the real axis and that those of $B$ lie on the imaginary axis, i.e., they are of the form \begin{align} \lambda_k^\uparrow(A)&=\alpha_k \\ \lambda_k^\uparrow(B)&=i\beta_k, \end{align} where $\alpha,\beta\in\mathbb{R}$ and where $\lambda^\uparrow(\cdot)$ lists the eigenvalues in ascending order, such that $\lambda_1^\uparrow(\cdot)\leq\lambda_2^\uparrow(\cdot)\dots\leq\lambda_n^\uparrow(\cdot).$
Proposition: The eigenvalues of $C$, $\lambda_k^\uparrow(C)=c_k=a_k+ib_k,$ lie within the rectangle extended by the eigenvalues of $A$ and $B,$ i.e., \begin{align} \alpha_1\leq &a_k \leq \alpha_n \\ \beta_1\leq &b_k \leq \beta_n \end{align} for all $k.$
How can we prove this?
Observation: It also seems that $\alpha\succ a$ and $\beta\succ b,$ where $\succ$ is the majorization preorder, as defined here. Perhaps this implies the proposition, while being easier to show?
Edit: It does imply the proposition, since $y\succ x$ iff $x$ is in the convex hull of all vectors obtained by permuting the coordinates of $y,$ so we can prove this instead.
Simulations support this, but so far, I can't even get started with a proof. I looked in Bhatia's Matrix Analysis, because I thought some of the many inequalities in it might help. I didn't find anything, but I must admit that much of it went a bit over my head, so something of use may very well be in there.
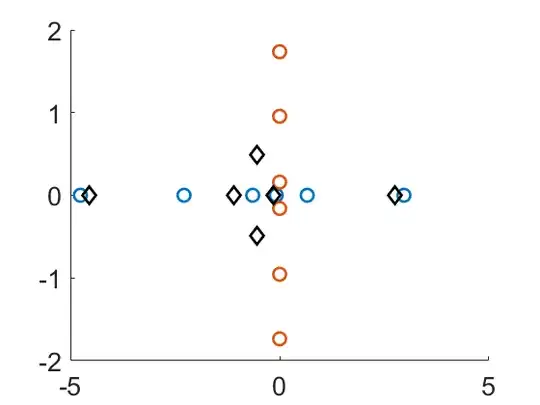
Here's an example of the eigenvalues of $A,B,C$ viewed in the complex plane, for $n=6,$ where we can see the eigenvalues of $C$ being within the rectangle extended by the min/max eigenvalue on either axis:
I tried loosening some of the demands on $A$ and $B,$ as seen in the table below, where a $1$ means that the demand is made and $0$ means that it isn't, but I found counter-examples to the proposition for all the listed variations with a $0.$
For all variations, $A$ ($B$) has exclusively real (imaginary) eigenvalues. So, for instance, if $A=DM_S$ is not demanded, then $A$ is simply an arbitrary matrix with exclusively real eigenvalues. \begin{array}{c|c|c|c|c|c|} & A=DM_S & B=DM_A & D\text{ is diagonal} & \lambda_k(D)\gtrless 0 \forall k & \text{Same }D\text{ for both }A,B \\ \hline \checkmark & 1 & 1 & 1 & 1 & 1 \\ \times & 0 & 1 & 1 & 1 & 1 \\ \times & 1 & 0 & 1 & 1 & 1 \\ \times & \vdots & \vdots & \vdots & \vdots & \vdots \end{array}
The motivation behind proving this proposition is to prove what I wrote about in this question.
Any input is highly appreciated!