22

Am I correct that homotopy groups of $U(N)$ and $SU(N)$ are the same, $$\pi_m(U(N))=\pi_m(SU(N)), \text{ for } m \geq 2$$ except that $$\pi_1(U(N))=\mathbb{Z}, \;\;\pi_1(SU(N))=0,$$

Hence the Table in page 3 of this note has error along the column of $\pi_1(U(N))$ which should be $\pi_1(U(N))=\mathbb{Z}$?

enter image description here

More generally, where can I find a trustworthy table for $\pi_m(U(N))$ and $\pi_m(SU(N))$?

I find additional results for $SU(N)$ here in this Ref:

enter image description here

wonderich
  • 6,059
  • 2
    Yes, that's right, and yes, $\pi_1$ should be $\mathbb{Z}$ for all $N$ in the table. – Qiaochu Yuan Oct 02 '17 at 22:46
  • Try Mimura's Article "The Homotopy Theory of Lie Groups", pg970, in James's "Handbook of Algebraic Topology" for a table of $\pi_iSU(n)$ for $i\leq15$, $n\leq 8$. He also gives references where some of the higher groups can be found. – Tyrone Oct 03 '17 at 07:54

1 Answers1

26

You are correct. This follows from the fact that $U(N)$ is diffeomorphic to $S^1\times SU(N)$. To see this, consider the map $f : U(N) \to S^1\times SU(N)$ given by $A \mapsto (\det A, \operatorname{diag}((\det A)^{-1}, 1, \dots, 1)A)$. This is a smooth map with smooth inverse given by $(z, B) \mapsto \operatorname{diag}(z, 1, \dots, 1)B$. Note however that the two groups are not isomorphic though (they have different centers), so they are not isomorphic as Lie groups.

As $SU(N)$ is simply connected, we see that

$$\pi_1(U(N)) = \pi_1(S^1\times SU(N)) = \pi_1(S^1)\oplus\pi_1(SU(N)) = \mathbb{Z}$$

and for $m \geq 2$,

$$\pi_m(U(N)) = \pi_m(S^1\times SU(N)) = \pi_m(S^1)\oplus\pi_m(SU(N)) = \pi_m(SU(N)).$$

As for your request regarding a table of the homotopy groups of $SU(N)$, the groups $\pi_m(SU(N))$ for $1 \leq m \leq 15$ and $1 \leq N \leq 8$ are given in appendix A, section 6, part VII of the Encyclopedic Dictionary of Mathematics. This doesn't quite cover all the cases you asked for in the comment below, but the missing ones follow from complex Bott periodicity.

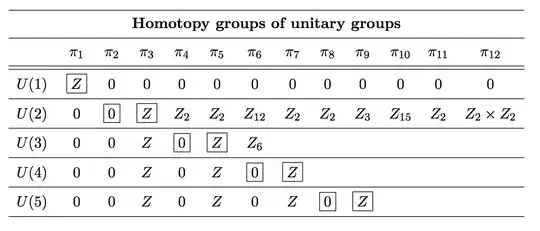
For completeness, here is the table you asked for.

\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline & \pi_1 & \pi_2 & \pi_3 & \pi_4 & \pi_5 & \pi_6 & \pi_7 & \pi_8 & \pi_9 & \pi_{10} & \pi_{11} & \pi_{12}\\ \hline SU(1) & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline SU(2) & 0 & 0 & \mathbb{Z} & \mathbb{Z}_2 & \mathbb{Z}_2 & \mathbb{Z}_{12} & \mathbb{Z}_2 & \mathbb{Z}_2 & \mathbb{Z}_3 & \mathbb{Z}_{15} & \mathbb{Z}_2 & \mathbb{Z}_2\oplus\mathbb{Z}_2 \\ \hline SU(3) & 0 & 0 & \mathbb{Z} & 0 & \mathbb{Z} & \mathbb{Z}_6 & 0 & \mathbb{Z}_{12} & \mathbb{Z}_3 & \mathbb{Z}_{30} & \mathbb{Z}_4 & \mathbb{Z}_{60} \\ \hline SU(4) & 0 & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & \mathbb{Z}_{24} & \mathbb{Z}_2 & \mathbb{Z}_{120}\oplus\mathbb{Z}_2 & \mathbb{Z}_4 & \mathbb{Z}_{60} \\ \hline SU(5) & 0 & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & \mathbb{Z}_{120} & 0 & \mathbb{Z}_{360}\\ \hline SU(6) & 0 & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & \mathbb{Z}_{720}\\ \hline SU(7) & 0 & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0\\ \hline SU(8) & 0 & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0\\ \hline SU(9) & 0 & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0\\ \hline SU(10) & 0 & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0 & \mathbb{Z} & 0\\ \hline \end{array}

Michael Albanese
  • 104,029
  • Dear Michael Albanese +1, Thanks. I will count you as an answer immediately if you can provide a much complete Table than mine ( if possible, say up to 12th homotopy group of SU(10), if there is a result done in math?). – wonderich Oct 03 '17 at 02:30
  • p.s. I mean a resource of Table up to 10 rows and 12 columns. – wonderich Oct 03 '17 at 02:31
  • 5
    The sequence $SU(N)\to U(N)\xrightarrow{\det}S^1$ is a fibration, and the corresponding long exact sequence of homotopy groups together with the vanishing of higher homotopy groups of $S^1$ gives this result without resorting to the unholy homeo :-) – Mariano Suárez-Álvarez Oct 03 '17 at 19:37
  • Dear professor, may I ask you a related question here? In particle physics, the weak interaction group is $SU(2)\times U(1)$, and I want to know the result of $\pi_1(SU(2)\times U(1))$? More generally, would $\pi_n(A\times B)=\pi_n(A)\otimes \pi_n(B)$? – Daren Jan 02 '24 at 11:50
  • 2
    @Daren: For path connected topological spaces $A$ and $B$, we have $\pi_n(A\times B) \cong \pi_n(A)\times\pi_n(B)$, see Proposition 4.2 of Hatcher's Algebraic Topology. Therefore $\pi_1(SU(2)\times U(1)) \cong \pi_1(SU(2))\times\pi_1(U(1)) \cong 0\times\mathbb{Z} \cong\mathbb{Z}$. – Michael Albanese Jan 03 '24 at 20:17
  • Could you elaborate a bit more on the difference between diffeomorphism and isomorphism in this particular case? You mentioned they have different centers, but I'm still a bit confused because diffeomorphism is isomorphism between differentiable manifolds. Thank you. – M. Zeng May 18 '24 at 06:51
  • 1
    @M.Zeng: Because they have different centers, the groups are not isomorphic. That is, the map $f$ is a diffeomorphism but not an isomorphism of groups, so while the manifolds are diffeomorphic, they are not isomorphic as Lie groups. – Michael Albanese May 18 '24 at 11:20